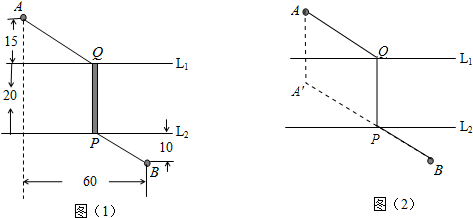
解:(1)作法:①将点A竖直向下平移到点A′,使AA′=20,
②连接A′B,与l
2交于点P,
③过点P作PQ⊥l
1于Q,
④连接AQ、BP.
则天桥建在PQ处能使由A经过天桥走到B的路程最短,如图;
(2)∵AA′∥PQ,AA′=PQ,
∴四边形AA′PQ是平行四边形,
∴AQ=A′P,
∴AQ+PB=A′P+PB=A′B.

过B作AA′的垂线,垂足为C.如图.
在△A′BC中,∠C=90°,BC=60,A′C=AC-AA′=15+20+10-20=25,
则A′B=
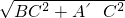
=65,
AQ+PQ+PB=A′B+PQ=65+20=85.
故由A经过天桥走到B的最短路线的长85米.
分析:(1)设天桥为PQ,则由A经过天桥走到B的最短路程为AQ+PQ+PB,由于PQ是定值,因此只需要考虑使AQ+PB最短.因为它们是分散的两条线段,故先将其中一条平移,如图平移AQ到A′P,此时连接A′B交l
2于P,得桥址;
(2)过B作AA′的垂线,垂足为C,则在△A′BC中,运用勾股定理求出A′B的长,则由A经过天桥走到B的最短路线的长:AQ+PQ+PB=A′B+PQ.
点评:本题主要考查了轴对称-最短路线问题,平行四边形的判定与性质,勾股定理,有一定难度,根据“两点之间,线段最短”找到桥址的位置是解题的关键.

 解:(1)作法:①将点A竖直向下平移到点A′,使AA′=20,
解:(1)作法:①将点A竖直向下平移到点A′,使AA′=20, 过B作AA′的垂线,垂足为C.如图.
过B作AA′的垂线,垂足为C.如图. =65,
=65,

 阅读快车系列答案
阅读快车系列答案 如图,网格中有一个四边形和两个三角形.
如图,网格中有一个四边形和两个三角形.