(1)解:∵正方形ABCD中,DQ=QC,P在BC上,且AP=CD+CP,
∴设PC=x,则BP=4-x,AP=4+x,
在Rt△ABP中,
∵AB
2+BP
2=AP
2,
∴4
2+(4-x)
2=(4+x)
2,
解得:x=1,
则BP=3,
AP=4+1=5;
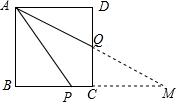
(2)证明:延长AQ交BC的延长线于M,
在△ADQ和△MCQ中,
∵
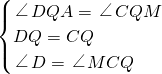
,
∴△ADQ≌△MCQ(ASA),
∴AD=CM,∠DAM=∠AMP,
∵AP=CD+CP,
∴AP=PM,
∴∠PAM=∠AMP,
∴∠DAM=∠PAM,
∵∠DAP=90°-∠BAP,
∴2∠DAQ=90°-∠BAP,
∴∠DAQ=45°-

∠BAP.
分析:(1)利用正方形性质以及DQ=QC,P在BC上,且AP=CD+CP,得出PC=x,则BP=4-x,AP=4+x,进而利用勾股定理求出即可;
(2)利用全等三角形的判定与性质首先得出△ADQ≌△MCQ,即可求出AD=CM,∠DAM=∠AMP,再利用等腰三角形的性质得出∠PAM=∠AMP,利用∠DAP=90°-∠BAP即可求出.
点评:此题主要考查了正方形的性质以及利用全等三角形的判定与性质和勾股定理等知识,利用已知正确作出辅助线延长AQ交BC的延长线于M是解题关键.

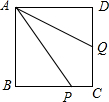 如图,已知正方形ABCD中,Q在CD上,且DQ=QC,P在BC上,且AP=CD+CP.
如图,已知正方形ABCD中,Q在CD上,且DQ=QC,P在BC上,且AP=CD+CP. ∠BAP.
∠BAP.
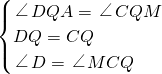 ,
, ∠BAP.
∠BAP.

 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.