
A、 | B、 | C、 | D、 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
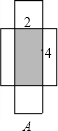
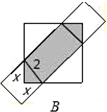
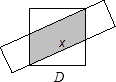
| x2-16 |
| 1 |
| 2 |
| x2-16 |
8(
| ||
| 3 |
8(
| ||
| 3 |
16(
| ||
| 3 |
| 2 |
| 7 |
| 2 |
16(
| ||
| 3 |
| 2 |
16(
| ||
| 3 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
 21、对某班学生一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请认真观察图形,并回答下列问题.
21、对某班学生一次数学测验成绩进行统计分析,各分数段的人数如图所示(分数取正整数),请认真观察图形,并回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 23、实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
23、实验中学现有学生2870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
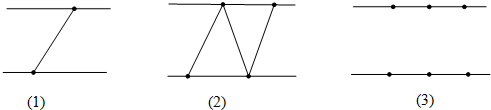
查看答案和解析>>
科目:初中数学 来源:2012-2013学年北京市顺义一中八年级(上)入学数学测试卷(解析版) 题型:解答题
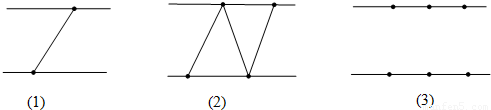
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com