
如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.

解:(1)设抛物线的解析式为y=ax2+bx+c
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.
把点A(1,0)、点B(﹣3,0)代入,得 解得a=﹣1,b=﹣2
解得a=﹣1,b=﹣2
∴抛物线的解析式为y=﹣x2﹣2x+3.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4
∴顶点D的坐标为(﹣1,4);
(2)△BCD是直角三角形.
理由如下:解法一:过点D分别作x轴、y轴的垂线,垂足分别为E、F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
 ∴CD2=DF2+CF2=2
∴CD2=DF2+CF2=2
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=DE2+BE2=20
∴BC2+CD2=BD2
∴△BCD为直角三角形.
解法二:过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3
∴OB=OC∴∠OCB=45°
∵在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1
∴DF=CF
∴∠DCF=45°
∴∠BCD=180°﹣∠DCF﹣∠OCB=90°
∴△BCD为直角三角形.
(3)①△BCD的三边, =
= =
= ,又
,又 =
= ,故当P是原点O时,△ACP∽△DBC;
,故当P是原点O时,△ACP∽△DBC;
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3﹣a, =
= ,即
,即 =
= ,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3﹣b,则 =
= ,即
,即 =
= ,解得:b=﹣
,解得:b=﹣ ,故P是(0,﹣
,故P是(0,﹣ )时,则△ACP∽△CBD一定成立;
)时,则△ACP∽△CBD一定成立;
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1﹣d,当AC与CD是对应边时, =
= ,即
,即 =
= ,解得:d=1﹣3
,解得:d=1﹣3 ,此时,两个三角形不相似;
,此时,两个三角形不相似;
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1﹣e,当AC与DC是对应边时, =
= ,即
,即 =
= ,解得:e=﹣9,符合条件.
,解得:e=﹣9,符合条件.
总之,符合条件的点P的坐标为: .
.


科目:初中数学 来源: 题型:
关于二次函数 ,以下结论:①不论
,以下结论:①不论 取何值,抛物线总经过点(1,0);②抛物线与
取何值,抛物线总经过点(1,0);②抛物线与 轴一定有两个交点;③若
轴一定有两个交点;③若
 6,抛物线交
6,抛物线交 轴于A、B两点,则AB
轴于A、B两点,则AB ;④抛物线的顶点在
;④抛物线的顶点在 图像上.上述说法错误的序号是____ _.
图像上.上述说法错误的序号是____ _.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:
①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(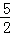 ,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A.①② B.②③ C.①②④ D.②③④
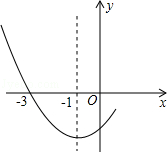
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com