
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
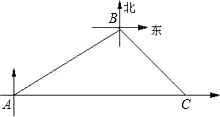
 会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:查看答案和解析>>
科目:初中数学 来源:2013届江苏省扬州市蒋王中学九年级下学期第一次模拟数学试卷(带解析) 题型:解答题
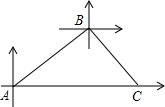
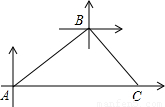
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求: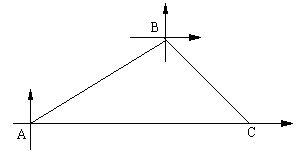
(1)港口A与小岛C之间的距离
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市九年级下学期第一次模拟数学试卷(解析版) 题型:解答题
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会和,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
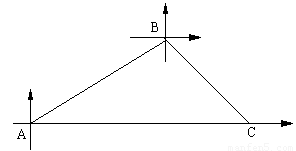
(1)港口A与小岛C之间的距离
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源:2013年山东省聊城市中考数学模拟试卷(七)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com