
已知:如图,直线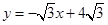 与x轴相交于点A,与直线
与x轴相交于点A,与直线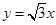 相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动(E不与点O,A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
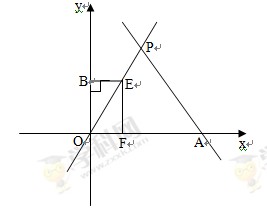
(1)求点P的坐标;
(2)请判断△OPA的形状并说明理由;
(3)请探究S与t之间的函数关系式,并指出t的取值范围.
(1) ;
;
(2)等边三角形;理由见解析;
(3) .
.
【解析】
试题分析:(1)由两直线相交可列出方程组,求出P点坐标;
(2)将y=0代入 ,可求出OA=4,作PD⊥OA于D,则OD=2,PD=
,可求出OA=4,作PD⊥OA于D,则OD=2,PD= ,利用tan∠POA=
,利用tan∠POA= ,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
,可知∠POA=60°,由OP=4.可知△POA是等边三角形;
(3)①当0<t≤4时,在Rt△EOF中,∠EOF=60°,OE=t,则EF= ,OF=
,OF= ,则S=
,则S= •OF•EF=
•OF•EF= ;
;
②当4<t<8时,设EB与OP相交于点C,易知:CE=PE=t﹣4,AE=8﹣t,可得AF=4﹣ ,EF=
,EF= (8﹣t),有OF=OA﹣AF=4﹣(4﹣
(8﹣t),有OF=OA﹣AF=4﹣(4﹣ )=
)= ,S=
,S= (CE+OF)•EF=﹣
(CE+OF)•EF=﹣ +4
+4 t﹣8
t﹣8 .
.
试题解析:(1)由题意可得: ,
,
解得 ,
,
所以点P的坐标为(2, );
);
(2)将y=0代入y=﹣ x+4
x+4 ,得到:﹣
,得到:﹣ x+4
x+4 =0,
=0,
∴x=4,即OA=4,
作PD⊥OA于D,则OD=2,PD=2 ,
,
∵tan∠POA= =
= ,
,
∴∠POA=60°,
∵OP= ,
,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,

∵∠EOF=60°,OE=t,
∴EF= ,OF=
,OF= ,
,
∴S= •OF•EF=
•OF•EF= .
.
②当4<t<8时,如图,设EB与OP相交于点C,

∵CE=PE=t﹣4,AE=8﹣t,
∴AF=4﹣ ,EF=
,EF= (8﹣t),
(8﹣t),
∴OF=OA﹣AF=4﹣(4﹣ )=
)= ,
,
∴S= (CE+OF)•EF=
(CE+OF)•EF= (t﹣4+
(t﹣4+ t)×
t)× (8﹣t)=
(8﹣t)=  .
.
考点:一次函数综合题.


科目:初中数学 来源: 题型:
(本题满分10分)
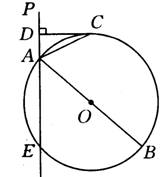
已知:如图直线PA交⊙O于A,E两点,过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C,连接AC,且AC平分∠DAB.
1. (1) 试判断DC与⊙O的位置关系?并说明理由.
2.(2) 若DC=4,DA=2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省扬州市武坚中学九年级第一学期期末考试数学卷 题型:解答题
(本题满分10分)
已知:如图直线PA交⊙O于A,E两点,过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C,连接AC,且AC平分∠DAB.
【小题1】(1) 试判断DC与⊙O的位置关系?并说明理由.
【小题2】(2) 若DC=4,DA=2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省扬州市九年级第一学期期末考试数学卷 题型:解答题
(本题满分10分)
已知:如图直线PA交⊙O于A,E两点,过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C,连接AC,且AC平分∠DAB.
1. (1) 试判断DC与⊙O的位置关系?并说明理由.
2.(2) 若DC=4,DA=2,求⊙O的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com