
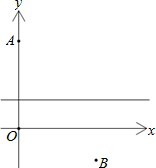 已知A和B两地在一条河的两岸,现在要在河上造一座桥MN(假定河的两岸是平行的,且桥要与河垂直),能够使得从A到B的路径AMNB最短.我们不妨将问题放在平面直角坐标系中来研究,如图A(0,7),B(6,-3).河的两岸分别设为y=2与x轴,那么从A到B的最短路径AMNB的长度为________.
已知A和B两地在一条河的两岸,现在要在河上造一座桥MN(假定河的两岸是平行的,且桥要与河垂直),能够使得从A到B的路径AMNB最短.我们不妨将问题放在平面直角坐标系中来研究,如图A(0,7),B(6,-3).河的两岸分别设为y=2与x轴,那么从A到B的最短路径AMNB的长度为________. 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 路将经过AB(线段),已知森林保护区的范围在以点P为圆心,半径为4km的圆形区域内.请问这条高速铁路会不会穿越保护区,为什么?
路将经过AB(线段),已知森林保护区的范围在以点P为圆心,半径为4km的圆形区域内.请问这条高速铁路会不会穿越保护区,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
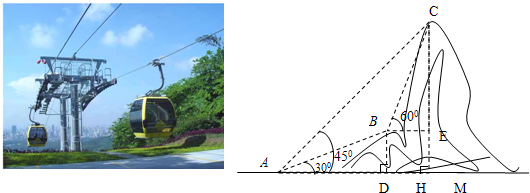
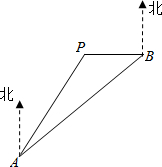
 (2012•景宁县模拟)如图所示,某市的A、B两地相距20km,B在A的北偏东45°方向上,一高新技术园区P在A的北偏东30°和B的正西方向上.现计划修建的一条高速铁路将经过AB(线段),已知高新技术园区的范围在以点P为圆心,半径为4km的圆形区域内.请通过计算回答:这条高速铁路会不会穿越高新技术园区?(参考数据:sin15°≈0.2588,cos15°≈0.9659,tan15°≈0.2679).
(2012•景宁县模拟)如图所示,某市的A、B两地相距20km,B在A的北偏东45°方向上,一高新技术园区P在A的北偏东30°和B的正西方向上.现计划修建的一条高速铁路将经过AB(线段),已知高新技术园区的范围在以点P为圆心,半径为4km的圆形区域内.请通过计算回答:这条高速铁路会不会穿越高新技术园区?(参考数据:sin15°≈0.2588,cos15°≈0.9659,tan15°≈0.2679).查看答案和解析>>
科目:初中数学 来源: 题型:
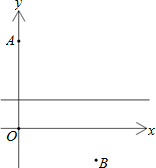 已知A和B两地在一条河的两岸,现在要在河上造一座桥MN(假定河的两岸是平行的,且桥要与河垂直),能够使得从A到B的路径AMNB最短.我们不妨将问题放在平面直角坐标系中来研究,如图A(0,7),B(6,-3).河的两岸分别设为y=2与x轴,那么从A到B的最短路径AMNB的长度为
已知A和B两地在一条河的两岸,现在要在河上造一座桥MN(假定河的两岸是平行的,且桥要与河垂直),能够使得从A到B的路径AMNB最短.我们不妨将问题放在平面直角坐标系中来研究,如图A(0,7),B(6,-3).河的两岸分别设为y=2与x轴,那么从A到B的最短路径AMNB的长度为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com