
分析 (1)先求出总的签数,再根据概率公式求出表演唱歌的概率和表演朗诵的概率,然后进行比较即可;
(2)根据概率公式求出进行到一半时表演唱歌、表演朗诵和表演舞蹈的概率,然后进行比较即可得出答案.
解答 解:(1)∵一共做了20张表演唱歌的签、12张表演朗诵的签、8张表演舞蹈的签,
∴抽到表演唱歌的概率是:$\frac{20}{20+12+8}$=$\frac{1}{2}$,
抽到表演朗诵的概率是$\frac{12}{20+12+8}$=$\frac{3}{10}$,
∴抽到表演唱歌和表演朗诵的可能性不相同;
(2)∵共做了20张表演唱歌的签、12张表演朗诵的签、8张表演舞蹈的签,
又∵已经有9人表演唱歌,6人表演朗诵、5人表演舞蹈,
∴剩下的表演唱歌的签有11张,表演朗诵的签有6张,表演舞蹈的签有3张,
∴这时去抽签,抽到表演唱歌的签的概率有$\frac{11}{20}$,表演朗诵的概率是$\frac{6}{20}$=$\frac{3}{10}$,表演舞蹈的概率是:$\frac{3}{20}$,
∴抽到表演舞蹈节目的可能性最小.
点评 此题考查了基本概率的计算及比较可能性大小,用到的知识点为:可能性等于所求情况数与总情况数之比.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
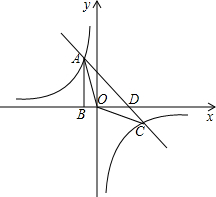 如图,点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$
如图,点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限内的交点,AB⊥x轴于B,且S△ABO=$\frac{3}{2}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
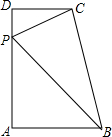 如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.
如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
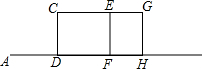 如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+5)和-5 | B. | -(-5)和5 | C. | (-$\frac{1}{2}$) 与-2 | D. | +|+8|和-(+8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com