
����Ŀ����ͼ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�2cm����A�㣬�������ƶ�3cm����B�㣬Ȼ�������ƶ�9cm����C�㣮
��1����1����λ���ȱ�ʾ1cm�������������ϱ�ʾ��A��B��C�����λ�ã� ![]()
��2���ѵ�C����A�ľ����ΪCA����CA=cm��
��3������B��ÿ��2cm���ٶ������ƶ���ͬʱA��C��ֱ���ÿ��1cm��4cm���ٶ������ƶ������ƶ�ʱ��Ϊt�룬��̽����CA��AB��ֵ�Ƿ������t�ı仯���ı䣿��˵�����ɣ�
���𰸡�
��1���⣺��ͼ��
![]()
��2��6
��3���⣺���䣬�������£�
���ƶ�ʱ��Ϊt��ʱ��
��A��B��C�ֱ��ʾ����Ϊ��2+t����5��2t��4+4t��
��CA=��4+4t��������2+t��=6+3t��AB=����2+t��������5��2t��=3+3t��
��CA��AB=��6+3t������3+3t��=3
��CA��AB��ֵ��������t�ı仯���ı�
���������⣺��2��CA=4������2��=4+2=6cm��
�����㾫����������Ĺؼ�����������������֪ʶ�����������ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ�ߣ��Լ��������ľ�������⣬�˽�ͬ����������룬���С����Ϊ֮������Ⱦ������㣬���������ˣ�ƽ�����������㣬���ݱ������ֵ�����ӿ�ƽ�������빫ʽҪ�μǣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����ABC��,��BAC=90��,AB=AC=6,DΪBC���е�.
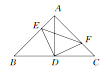
(1)��E,F�ֱ���AB,AC�ϵĵ�,��AE=CF,��֤:��AED�ա�CFD;
(2)����F,E�ֱ��C,A����ͬʱ����,��ÿ��1����λ���ȵ��ٶ���CA,AB�˶�,����A,Bʱֹͣ;����DEF�����Ϊy,F���˶���ʱ��Ϊx,��y��x�ĺ�����ϵʽ;
(3)��(2)��������,��F,E�ֱ���CA,AB���ӳ������˶�,���ʱy��x�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������εĶ���Ϊ80���������ĵǶ���Ϊ��������
A. 80�� B. 50�� C. 40�� D. 20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A.��a+b��2=a2+b2B.��-2ab3��3=-6a3b6
C.��-a+b����a+b��=b2-a2D.2x2y+3xy2=5x3y3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϵ�A��ʾ�����ǣ�5����B��ʾ������7����A��B�����ľ�����
A. 2 B. ��12 C. 12 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����У���ȷ���ǣ�������
A. x3x2=x4 B. ��x+y����x��y��=x2+y2
C. x��x��2��=��2x+x2 D. 3x3y2��xy2=3x4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������ڵ�����������Ϊm��n��p��������p=m2��n����������Ϊ��1��3����2��a����7��b������b=
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com