
解:(1)令x=0,则y=3.
∴B点坐标为(0,3),OB=3.
∵tan∠OAB=

,
∴AO=1.
∴A点坐标为(-1,0).
∴0=(-1)
2+b(-1)+3.
求得b=4.
∴所求的抛物线解析式为y=x
2+4x+3.
(2)设平移后抛物线的解析式为y=x
2+4x+3+k.
∵它经过点(-5,6),
∴6=(-5)
2+4(-5)+3+k.
∴k=-2.
∴平移后抛物线的解析式为y=x
2+4x+3-2=x
2+4x+1.
配方,得y=(x+2)
2-3.
∵a=1>0,
∴平移后的抛物线的最小值是-3.
(3)由(2)可知,BD=PQ=2,对称轴为x=-2.
又S
△MBD=2S
△MPQ,
∴BD边上的高是PQ边上的高的2倍.
设M点坐标为(m,n).
①当M点的对称轴的左侧时,则有0-m=2(-2-m).
∴m=-4.
∴n=(-4)
2+4(-4)+1=1.
∴M(-4,1).
②当M点在对称轴与y轴之间时,则有0-m=2[m-(-2)].
∴m=-

.
∴n=(-

)
2+4(-

)+1=-
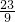
.
∴M(-

,-
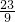
).
③当M点在y轴的右侧时,则有m=2[(m-(-2)].
∴m=-4<0,不合题意,应舍去.
综合上述,得所求的M点的坐标是(-4,1)或(-

,-
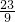
).
分析:(1)根据抛物线的解析式即可得出B点的坐标为(0,3),即OB=3,在直角三角形OAB中,根据OB的长和∠ABO的正切值即可求出OA的长,也就能得知A点的坐标,然后根据A点的坐标即可求出抛物线的解析式.
(2)可用k表示出平移后抛物线的解析式,已知了平移后的抛物线过点C(-5,6),那么可将C点的坐标代入其中,即可求出k的值.进而可根据得出的二次函数求出其最小值.
(3)本题要先求出BD和PQ的长,根据(2)可得出BD=PQ=2,因此要使△MBD的面积是△MPQ面积的2倍,只需让M到y轴的距离等于M到抛物线对称轴(即PQ)的距离的2倍即可.因此本题可分三种情况进行讨论:
①M在抛物线对称轴和y轴的左侧时;②M在抛物线对称轴和y轴之间;③M在y轴和抛物线对称轴右侧时.
根据上述三种情况可得出三个不同的M点的横坐标,将其代入抛物线的解析式中即可得出M点的坐标.
点评:本题着重考查了待定系数法求二次函数解析式、二次函数图象的平移、三角形面积的计算方法等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

 点B,tan∠ABO=
点B,tan∠ABO= ,顶点为P.
,顶点为P. ,顶点坐标是
,顶点坐标是 .
. 解:(1)令x=0,则y=3.
解:(1)令x=0,则y=3. ,
, .
. )2+4(-
)2+4(- )+1=-
)+1=-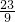 .
. ,-
,-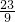 ).
). ,-
,-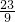 ).
).


 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: