解:(1)证明:∵直径AB⊥CD,OF⊥BD,
∴CD=2CE,BD=2BF,且∠CEO=∠BFO=90°,
在△OEC与△OFB中,
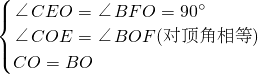
,
∴△OEC≌△OFB(AAS),
∴CE=BF,
∴BD=CD;
(2)在Rt△CFD中,DF=

BD=

CD,
∴∠C=30°,
∴CE=OC•cos30°=4×

=2

,
∴CD=2CE=2×2

=4

;
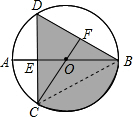
(3)如图,连接BC,
∵∠OCE=30°,CF⊥BD,
∴∠D=60°,∠BOC=120°,
又∵CD=BD,
∴△BCD是等边三角形,
∴S
阴影=S
△BCD+S
扇形OBC-S
△OBC,
=

×(4

)
2•sin60°+
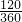
×π•4
2-

OB•CE
=

×48×

+

π-

×4×2

=12

+

π-4

=8

+

π.
分析:(1)先根据垂径定理可得CD=2CE,BD=2BF,然后利用角角边证明△OEC与△OFB全等,根据全等三角形对应边相等可得CE=BF,从而得解;
(2)根据直角三角形30°角所对的直角边等于斜边的一半可得∠C=30°,然后利用余弦定义求出CE的长度,再根据垂径定理即可的解;
(3)连接BC,根据(2)中结论可证△BCD是等边三角形,则阴影部分的面积=等边三角形BCD的面积+扇形OBC的面积-△OBC的面积,然后列式进行计算即可求解.
点评:本题考查了垂径定理,全等三角形的判定与性质,以及扇形的面积公式,30°角所对的直角边等于斜边的一半的性质,难度不大,(1)中证明三角形全等是解题的关键.

 如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,
如图,已知⊙O的直径AB垂直于点E,连接CO并延长交BD于点F,若CF⊥BD,AB=8,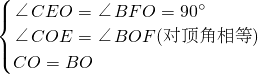 ,
, BD=
BD= CD,
CD, =2
=2 ,
, =4
=4 ;
;
 ×(4
×(4 )2•sin60°+
)2•sin60°+ ×π•42-
×π•42- OB•CE
OB•CE ×48×
×48× +
+ π-
π- ×4×2
×4×2
 +
+ π-4
π-4
 +
+ π.
π.
