
 x2+bx+c��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0��-1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ�
x2+bx+c��b��cΪ�������Ķ���ΪP������ֱ��������ABC�Ķ���A������Ϊ��0��-1����C������Ϊ��4��3����ֱ�Ƕ���B�ڵ������ޣ� �Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
�Ƿ�������ֵ�������ڣ���������ֵ���������ڣ���˵�����ɣ�
 ����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x-5���������ߵĽ��㣬��Ϊ����֮M�㣻
����ʱ����ֱ��AC����ƽ��4����λ������ֱ�ߣ�y=x-5���������ߵĽ��㣬��Ϊ����֮M�㣻 ����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x-3���������ߵĽ��㣬��Ϊ����֮M�㣮
����ʱ����ֱ��AC����ƽ��2����λ������ֱ�ߣ�y=x-3���������ߵĽ��㣬��Ϊ����֮M�㣮 Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ��
Ϊ��ֵ����˵�NP+BQȡ��Сֵʱ�� �����ֵ��
�����ֵ�� ����ã�b=2��c=-1��
����ã�b=2��c=-1�� x2+2x-1��
x2+2x-1�� ��x-m��2+m-1��
��x-m��2+m-1�� ��
�� ��
��
 =AP��
=AP�� ����ΪPQ�ij�����
����ΪPQ�ij�����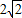 ��
�� x2+2x-1�ڵ�M����MΪ���������ĵ㣮
x2+2x-1�ڵ�M����MΪ���������ĵ㣮 ���ã�
���ã�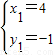 ��
��

 ��
�� ��
��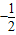 x2+2x-1�ڵ�M����MΪ���������ĵ㣮
x2+2x-1�ڵ�M����MΪ���������ĵ㣮 ���ã�
���ã� ��
��
 ��-2+
��-2+ ����M4��1-
����M4��1- ��-2-
��-2- ����
���� ��-2+
��-2+ ����M4��1-
����M4��1- ��-2-
��-2- ����
���� �������ֵ���������£�
�������ֵ���������£� Ϊ��ֵ����NP+BQȡ��Сֵʱ��
Ϊ��ֵ����NP+BQȡ��Сֵʱ�� �����ֵ��
�����ֵ��
 =
= ��
�� ��
�� �����ֵΪ
�����ֵΪ =
= ��
��

 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
����ԭ�㣮A��B����ĺ�����ֱ��Ƿ���x2-4x-12=0����������cos��DAB=
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任��
18����ƽ��ֱ������ϵ�У���һ��ͼ��������ԭ��˳ʱ����ת�ĽǶ�Ϊ�ȣ�����ԭ��Ϊλ�����ģ����Ʊ�Ϊk�õ�һ���µ�ͼ�Σ����ǰ�������̼�Ϊ���ȣ�k���任�����磬��ͼ�еġ�ABC������ԭ��O˳ʱ����ת�ĽǶ�Ϊ90�㣬����ԭ��Ϊλ�����ģ����Ʊ�Ϊ2�õ�һ���µ�ͼ�Ρ�A1B1C1������������̼�Ϊ��90�㣬2���任���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com