
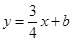 与抛物线
与抛物线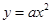 交于点A(1,
交于点A(1,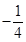 ),与
),与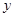 轴交于点C.
轴交于点C.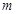 个单位(
个单位(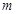 >0),抛物线与
>0),抛物线与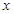 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求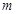 的值;
的值;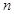 个单位(
个单位(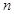 >0),抛物线与
>0),抛物线与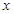 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时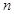 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.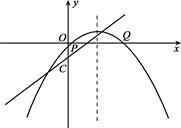
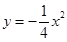 ,C(0,-1);(2)
,C(0,-1);(2)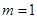 ;(3)最小值为
;(3)最小值为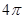 ,
,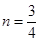
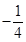 )分别代入直线
)分别代入直线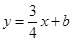 与抛物线
与抛物线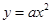 ,即可求得结果;
,即可求得结果;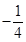 )分别代入直线
)分别代入直线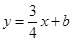 与抛物线
与抛物线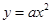 ,
,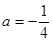 ,
,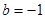 ,
,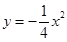 ,直线的解析式为,
,直线的解析式为,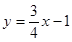 中,当
中,当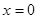 时,
时,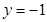 ,
,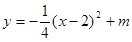 ,
,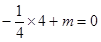 ,解得
,解得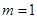 ;
;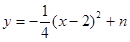 ,
,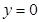 ,则
,则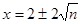 ,
,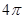 ,
,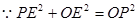 ,
,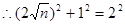 ,解得
,解得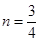 ,
, 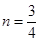 时,过C、P、Q三点的圆的面积最小,最小面积为
时,过C、P、Q三点的圆的面积最小,最小面积为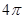 .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:不详 题型:解答题
 米.请你建立适当的平面直角坐标系解决下列问题.
米.请你建立适当的平面直角坐标系解决下列问题. 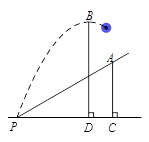
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | …[ | -6 | 0 | 4 | 6 | 6 | … |
| | | | | | | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
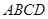 中,
中,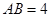 cm,
cm,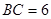 cm,现有一动点
cm,现有一动点 从
从 出发以2cm/秒的速度,沿矩形的边
出发以2cm/秒的速度,沿矩形的边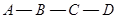 回到点
回到点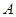 ,设点
,设点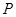 运动的时间为
运动的时间为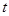 秒.
秒.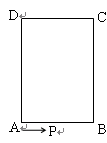
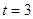 秒时,求
秒时,求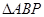 的面积;
的面积;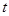 为何值时,点
为何值时,点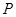 与点
与点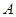 的距离为5cm?
的距离为5cm?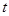 为何值时
为何值时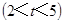 ,以线段
,以线段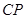 、
、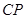 、
、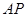 的长度为三边长的三角形是直角三角形,且
的长度为三边长的三角形是直角三角形,且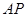 是斜边.
是斜边.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
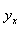 表示与自变量
表示与自变量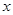 所对应的函数值。例如对于函数
所对应的函数值。例如对于函数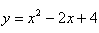 ,当
,当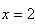 时,对应的函数值
时,对应的函数值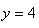 ,则可以写为:
,则可以写为: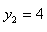 。在二次函数
。在二次函数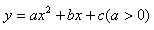 中,若
中,若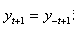 对任意实数
对任意实数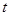 都成立,那么下列结论错误的是( )
都成立,那么下列结论错误的是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com