
分析 联立两直线解析式求出交点坐标,再根据交点在第四象限列出不等式组求解即可.
解答 解:联立$\left\{\begin{array}{l}{y=-2x+b}\\{y=2x-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{b+1}{4}}\\{y=\frac{b-1}{2}}\end{array}\right.$,
∵交点在第四象限,
∴$\left\{\begin{array}{l}{\frac{b+1}{4}>0①}\\{\frac{b-1}{2}<0②}\end{array}\right.$,
解不等式①得,b>-1,
解不等式②得,b<1,
所以,b的取值范围是-1<b<1.
故答案为:-1<b<1.
点评 本题考查了两直线相交的问题,解答此题的关键是解一元一次不等式组,联立两函数解析式求交点坐标是常用的方法,要熟练掌握并灵活运用.


科目:初中数学 来源: 题型:选择题
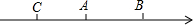 如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )
如图,数轴上A、B两点表示的数分别为-1和$\sqrt{3}$,点A是BC的中点,则点C所表示的数( )| A. | -2-$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
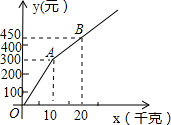 甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
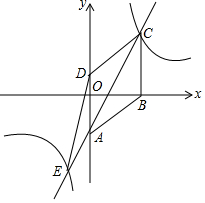 已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.
已知四边形ABCD是菱形,在平面直角坐标系中的位置如图,边AD经过原点O,已知A(0,-3),B(4,0),反比例函数图象经过点C,直线AC交双曲线另一支于点E,连接DE,CD,设反比例函数解析式为y1=$\frac{k}{x}$,直线AC解析式为y2=ax+b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com