
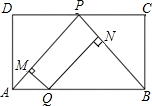
 (2012•烟台)如图,矩形ABCD中,P为CD中点,点Q为AB上的动点(不与A,B重合).过Q作QM⊥PA于M,QN⊥PB于N.设AQ的长度为x,QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是( )
(2012•烟台)如图,矩形ABCD中,P为CD中点,点Q为AB上的动点(不与A,B重合).过Q作QM⊥PA于M,QN⊥PB于N.设AQ的长度为x,QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是( )| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PE•AB |
| PB |
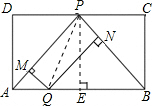 解:连接PQ,作PE⊥AB垂足为E,
解:连接PQ,作PE⊥AB垂足为E,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PE•AB |
| PB |
| PE•AB |
| PB |


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
 (2012•烟台)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为h1.若将横板AB换成横板A′B′,且A′B′=2AB,O仍为A′B′的中点,设B′点的最大高度为h2,则下列结论正确的是( )
(2012•烟台)如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为h1.若将横板AB换成横板A′B′,且A′B′=2AB,O仍为A′B′的中点,设B′点的最大高度为h2,则下列结论正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•烟台)如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°.
(2012•烟台)如图,在平面直角坐标系中,A,B两点的纵坐标分别为7和1,直线AB与y轴所夹锐角为60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com