Question

16．已知，如图（1），在矩形OABC中，OA=12，OC=9，以O为坐标原点，OC所在直线为x轴，建立平面直角坐标系，Rt△DEF中，点D与点O重合，∠DEF=90°，DF=$\frac{25}{4}$，DE=5，∠AOB=∠FOE．
（1）填空：直线OB的解析式为y=$\frac{4}{3}$x；图（1）点E的坐标是（3，-4）；
（2）如图（2），若将△DEF沿着射线OB方向平移，设平移的距离为k，当点E恰好平移到线段OC上时，求平移的距离k的值；
（3）在（2）问的情况下，即当点E平移到线段OC上时，是否存在直线OB上的点M和线段BC上的点N，使以D，E，M，N为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，说明理由；
（4）如图（3），直线AK：y=x+b经过点A，如果点P在y轴上，且位于点A的下方，点G在直线AK上，是否存在射线OB上点Q，使得以A、P、Q、G为顶点的四边形是菱形？若存在，请求出Q点的横坐标；简要说明理由；若不存在，请简要说明理由．

Answer 1

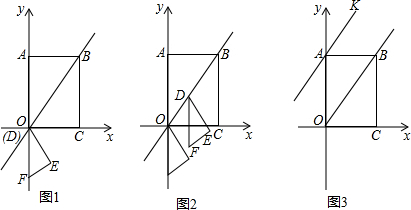
分析 （1）如图1中，作EM⊥OF于M．利用待定系数法可以确定直线OB解析式，根据$\frac{1}{2}$DF•EM=$\frac{1}{2}$•DE•EF，求出EM，即可求出点E坐标．
（2）如图2中，由DM∥BC，得$\frac{OM}{OC}$=$\frac{DM}{BC}$，求出OM即可解决问题．
（3）存在．分两种情形①如图3中，当DE为平行四边形DENM的边时，作MF⊥BC于F．②如图4中，当DE为平行四边形DNEM的对角线时，DE交ON于F．分别求出点坐标即可．
（4）存在．分两种情形①如图5中，四边形AGQP是菱形时，AG=GQ，设Q（m，$\frac{4}{3}$m），②如图6中，四边形AGPQ是菱形时，PA交GQ于点D，分别列出方程即可解决问题．

解答 解：（1）如图1中，作EM⊥OF于M．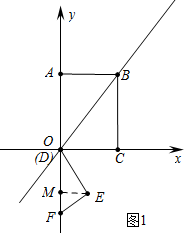

设OB解析式为y=kx，把B（9，12）代入得12=9k，
∴k=$\frac{4}{3}$，
∴直线OB解析式为y=$\frac{4}{3}$x，
 在Rt△DEF中，∵∠DEF=90°，DF=$\frac{25}{4}$，DE=5，
∴EF=$\sqrt{D{F}^{2}-D{E}^{2}}$=$\frac{15}{4}$，
∴$\frac{1}{2}$DF•EM=$\frac{1}{2}$•DE•EF，
∴EM=3，
∴OM=$\sqrt{D{E}^{2}-E{M}^{2}}$=4，
∴点E坐标（3，-4），
故答案分别为y=$\frac{4}{3}$x，（3，-4）．

（2）如图2中，当点E在OC上时，由（1）可知，EM=3．DM=4，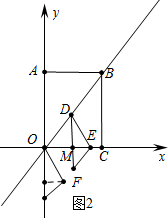

∵DM∥BC，
∴$\frac{OM}{OC}$=$\frac{DM}{BC}$，
∴OM=$\frac{DM•OC}{BC}$=$\frac{4×9}{12}$=3，
∴OD=$\sqrt{O{M}^{2}+D{M}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴当点E恰好平移到线段OC上时，求平移的距离k为5．

（3）存在，理由如下：
①如图3中，当DE为平行四边形DENM的边时，作MF⊥BC于F．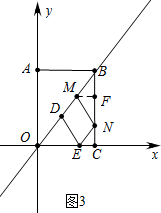

∵DE=MN=5，∠MNB=∠MBN，
∴MB=MN=5，
∵MF∥OC，
∴$\frac{MF}{OC}$=$\frac{MB}{BO}$，
∴MF=$\frac{BM•CO}{BO}$=$\frac{5×9}{15}$=3，
∴BF=$\sqrt{M{B}^{2}-M{F}^{2}}$=4，
∴点M坐标（6，8）．
②如图4中，当DE为平行四边形DNEM的对角线时，DE交ON于F．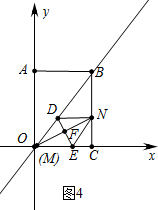

∵点F坐标（4.5，2），设点M坐标为（x，y），
则4.5=$\frac{x+9}{2}$，
∴x=0，
∴点M坐标为（0，0），
综上所述D，E，M，N为顶点的四边形是平行四边形时，点M坐标为（0，0）或（6.8）．

（4）存在，理由如下：
①如图5中，四边形AGQP是菱形时，AG=GQ，设Q（m，$\frac{4}{3}$m），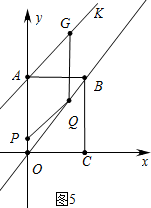

∵直线AK解析式y=x+b经过A（0，12），
∴b=12，
∴直线AK解析式为y=x+12，
∴点G坐标（m，m+12），
∴$\sqrt{2}$m=m+12-$\frac{4}{3}$m．
∴m=$\frac{36（3\sqrt{2}-1）}{17}$．
②如图6中，四边形AGPQ是菱形时，PA交GQ于点D，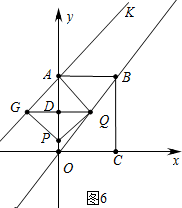

∵∠GAD=45°，
∴∠QAD=∠DAQ=45°，
∴∠GAQ=90°，
∴四边形GAQP是正方形，设Q（m，$\frac{4}{3}$m），
∵DQ∥AB，
∴$\frac{DQ}{AB}$=$\frac{OD}{OA}$，
∴$\frac{m}{9}$=$\frac{12-m}{12}$，
∴m=$\frac{36}{7}$，
综上所述A、P、Q、G为顶点的四边形是菱形时，点Q的横坐标为$\frac{36}{7}$或$\frac{36（3\sqrt{2}-1）}{17}$．

点评 本题考查一次函数综合题、平行四边形、矩形、菱形的判定和性质等知识，解题的关键是学会分类讨论，需要正确画好图象，学会把问题转化为方程解决，属于中考压轴题．