
| A. | $\sqrt{{x}^{2}+1}$ | B. | x$\sqrt{\frac{y}{x}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{1\frac{1}{2}}$ |
分析 结合最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.求解即可.
解答 解:A、$\sqrt{{x}^{2}+1}$是最简二次根式,本选项正确;
B、x$\sqrt{\frac{y}{x}}$=$\sqrt{xy}$,不是最简二次根式,本选项错误;
C、$\sqrt{12}$=2$\sqrt{3}$,不是最简二次根式,本选项错误;
D、$\sqrt{1\frac{1}{2}}$=$\frac{\sqrt{6}}{2}$,不是最简二次根式,本选项错误.
故选A.
点评 本题考查了最简二次根式,解答本题的关键在于熟练掌握最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则a2=b2 | B. | 对顶角相等 | ||
| C. | 若(a+1)x>(a+1),则x>1 | D. | 三角形中,等边对等角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 38 | B. | 40 | C. | 42 | D. | 44 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
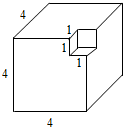 如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )| A. | 变大了 | B. | 变小了 | C. | 没变 | D. | 无法确定变化 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=97,n=4 | B. | m=9.7,n=4 | C. | m=97,n=5 | D. | m=9.7,n=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com