
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
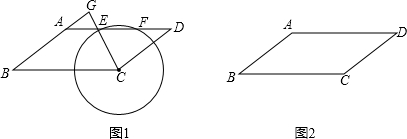
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
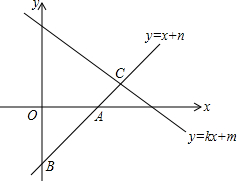 如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论:
如图,直线AB的解析式为y=x+n与直线y=kx+m交于C点(其中k,m,n为常数)点C的横坐标为3,下列四个结论:| A. | ①②③ | B. | ①②④ | C. | 只有②④ | D. | 只有①④ |
查看答案和解析>>
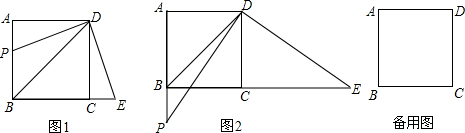
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
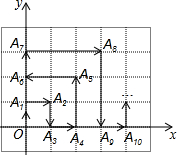 如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).
如图,在一单位为1的方格纸上建立直角坐标系,动点P按图中箭头所示方向运动,第一次从原点运动到点A1(0,1),第二次运动到点A2(1,1),第三次接着运动到点A3(1,0),…,按这样的运动规律,经过第2014次运动后,动点P运动到的点A2014的坐标是(672,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
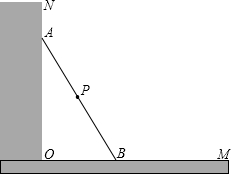 如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com