
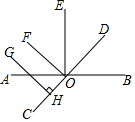
 如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO.
如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO. 分析 根据角平分线的定义得到∠DOE=$\frac{1}{2}∠$BOE,∠EOF=$\frac{1}{2}∠$AOE,根据垂直的定义得到∠GHO=∠FOD,根据平行线的判定定理即可得到结论.
解答 证明:∵OD平分∠EOB,
∴∠DOE=$\frac{1}{2}∠$BOE,
∵OF平分∠AOE,
∴∠EOF=$\frac{1}{2}∠$AOE,
∴∠FOD=∠DOE+∠EOF=$\frac{1}{2}$(∠AOE+∠BOE)=90°,
∵GH⊥CD,
∴∠GHO=90°,
∴∠GHO=∠FOD,
∴GH∥FO.
点评 本题考查了角平分线的定义,平行线的判定,熟练掌握平行线的判定是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 11×104 | B. | 1.1×105 | C. | 1.1×104 | D. | 0.11×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
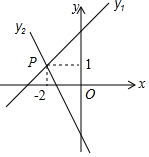 定义运算min{a,b}:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{-3,-1}=-3.根据该定义运算完成下列问题:
定义运算min{a,b}:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a;如:min{4,0}=0;min{2,2}=2;min{-3,-1}=-3.根据该定义运算完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
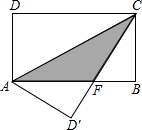 如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=24,BC=12,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )| A. | 60 | B. | 80 | C. | 100 | D. | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A和事件B都是必然事件 | |
| B. | 事件A是随机事件,事件B是不可能事件 | |
| C. | 事件A是必然事件,事件B是随机事件 | |
| D. | 事件A和事件B都是随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
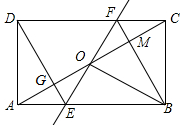 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com