
如图1,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a,h,且是关于x的一元二次方程mx2+nx+k=0的两个实数根,设过D,E,F三点的⊙O的面积为S⊙O,矩形PDEF的面积为S矩形PDEF.
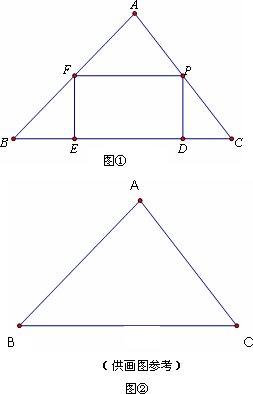
(1)求证:以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4;
(2)求![]() 的最小值;
的最小值;
(3)当![]() 的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m,n,k的取值是否有关?请说明理由.
的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m,n,k的取值是否有关?请说明理由.
|
解:解法一: (1)据题意,∵a+h= ∴所求正方形与矩形的面积之比: ∵n2-4mk≥0,∴n2≥4mk,由 (说明:此处未得出mk>0只扣1分,不再影响下面评分) ∴ 即正方形与矩形的面积之比不小于4. (2)∵∠FED=90°,∴DF为⊙O的直径. ∴⊙O的面积为: 矩形PDEF的面积:S矩形PDEF=EF·DE. ∴面积之比: ∵ ∴ (3)当 过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP=e, ∵BN∥FE,NF∥BE,∴BN=EF,∴BN=FP=e. 由BC∥MQ,得:BM=AG=h. ∵AQ∥BC,PF∥BC,∴AQ∥FP, ∴△FBP∽△ABQ. 8分 (说明:此处有多种相似关系可用,要同等分步骤评分) ∴ ∴ ∴线段AQ的长与m,n,k的取值有关. (解题过程叙述基本清楚即可)
解法二: (1)∵a,h为线段长,即a,h都大于0, ∴ah>0 1分(说明:此处未得出ah>0只扣1分,再不影响下面评分) ∵(a-h)2≥0,当a=h时等号成立. 故,(a-h)2=(a+h)2-4ah≥0. 2分 ∴(a+h)2≥4ah, ∴ 这就证得 (2)设矩形PDEF的边PD=x,DE=y,则⊙O的直径为 S⊙O= = 由(1), ∴ ∴ (3)当 这时矩形PDEF的四边相等为正方形. ∴EF=PF.作AG⊥BC,G为垂足. ∵△AGB∽△FEB,∴ ∵△AQB∽△FPB, ∴ 而EF=PF,∴AG=AQ=h,10分 ∴AG=h= 或者AG=h= ∴线段AQ的长与m,n,k的取值有关. (解题过程叙述基本清楚即可)
|


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
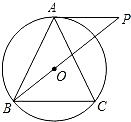 如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:
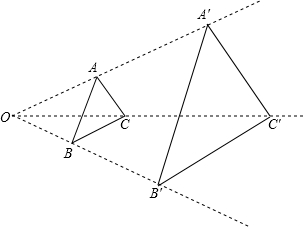
| OA′ |
| OA |
| OB′ |
| OB |
| OC′ |
| OC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com