Question

如图，一圆锥的底面半径为2，母线PB的长为6，D为PB的中点．一只蚂蚁从点A出发，沿着圆锥的侧面爬行到点D，则蚂蚁爬行的最短路程为

1. A.
   
2. B.
   2
3. C.
   3
4. D.
   3

Answer 1

C

分析：要求蚂蚁爬行的最短距离，需将圆锥的侧面展开，进而根据“两点之间线段最短”得出结果．
解答：由题意知，底面圆的直径AB=4，
故底面周长等于4π．
设圆锥的侧面展开后的扇形圆心角为n°

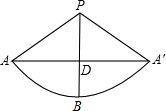
根据底面周长等于展开后扇形的弧长得4π=，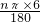
解得n=120°，
所以展开图中∠APD=120°÷2=60°，
因为半径PA=PB，∠APB=60°，
故三角形PAB为等边三角形，
又∵D为PB的中点，
所以AD⊥PB，在直角三角形PAD中，PA=6，PD=3，
根据勾股定理求得AD=3，
所以蚂蚁爬行的最短距离为3．
故选C．
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把圆锥的侧面展开成扇形，“化曲面为平面”，用勾股定理解决．