练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．当x=-4时，二次三项式ax2-4x-1的值是-1，求当x=5时，这个二次三项式的值．

    分析 首先根据当x=-4时，二次三项式ax2-4x-1的值是-1，求出a的值是多少；然后应用代入法，求出当x=5时，这个二次三项式的值是多少即可．

    解答 解：∵当x=-4时，二次三项式ax2-4x-1的值是-1，
    ∴a×（-4）2-4×（-4）-1=-1，
    整理，可得16a+15=-1，
    解得a=-1，
    ∴当x=5时，
    -x2-4x-1
    =-52-4×5-1
    =-25-20-1
    =-46

    点评 此题主要考查了代数式求值问题，要熟练掌握，求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值．题型简单总结以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．在平面直角坐标系中，对于任意一点P（x，y），我们做以下规定：d（P）=|x|+|y|，称d（P）为点P的坐标距离．
    （1）已知：点A（3，-4），求点A的坐标距离d（A）的值．
    （2）如图，四边形OABC为矩形，点A，B在第一象限，且OC：OA=1：2．
    ①求证：d（A）=d（C）×2
    ②若OC=2，且满足d（A）+d（C）=d（B）+2，求点B坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，DE，BC被那条直线所截，得到哪些同位角，内错角或同旁内角？请一一指出．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

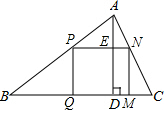    9．如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成长方形零件PQMN，使长方形PQMN的边QM在BC上，其余两个顶点P，N分别在AB，AC上，求这个长方形零件PQMN面积S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知x=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$，y=$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$，求x2-y2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．一艘客船从A地出发到B地顺流行驶，用了2.5小时；从B地返回A地逆流行驶，用了3.5小时，已知水流的速度是4千米/小时，求客船在静水中的平均速度？（用一元一次方程解）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．△ABC为等腰直角三角形，∠ABC=90°，点D在AB边上（不与点A、B重合），以CD为腰作等腰直角△CDE，∠DCE=90°．
    （1）如图1，作EF⊥BC于F，求证：△DBC≌△CFE；
    （2）在图1中，连接AE交BC于M，求$\frac{AD}{BM}$的值；
    （3）如图2，过点E作EH⊥CE交CB的延长线于点H，过点D作DG⊥DC，交AC于点G，连接GH，当点D在边AB上运动时，探究线段HE，HG与DG之间的数量关系，并证明你的结伦．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．建立下列问题中的方程模型：
    （1）把1 500元奖学金按照两种等级奖励给24名学生，其中一等奖每人200元，二等奖每人50元，获得一等奖的学生有多少人？
    （2）张晓买了8个莲蓬，付款50元，找回38元，每个莲蓬多少钱？
    （3）一个正方形花圃的边长增加2m，所得新正方形花圃的周长是28m，则原正方形花圃的边长是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．一辆汽车从A地驶往B地，前三分之一路段为普通公路，其余路段为高速公路．已知汽车在普通公路上行驶的速度为60km/h，在高速公路上行驶的速度为100km/h，汽车从A地到B地一共行驶了2.2h，求A、B两地的距离．

    查看答案和解析>>

    同步练习册答案