
正方形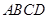 的边长为4,
的边长为4,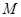 、
、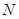 分别是
分别是 、
、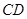 上的两个动点,当
上的两个动点,当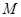 点在
点在 上运动时,始终保持
上运动时,始终保持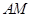 和
和 垂直,
垂直,
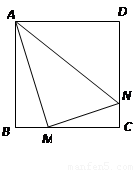
(1)证明: ;
;
(2)设 ,梯形
,梯形 的面积为
的面积为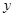 ,求
,求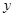 与
与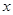 之间的函数关系式;当
之间的函数关系式;当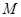 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;
(3)当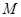 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.
(1)证明见解析(2)当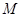 点为BC中点时,四边形
点为BC中点时,四边形 面积最大,最大面积是10(3)当点
面积最大,最大面积是10(3)当点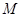 运动到
运动到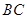 的中点时,
的中点时, ,
,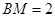
【解析】证明(1)在正方形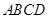 中
中
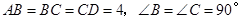
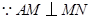
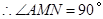
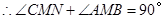
在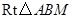 中,
中,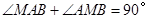
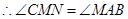
 ··························· 4分
··························· 4分
(2)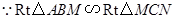
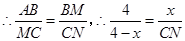
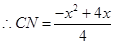
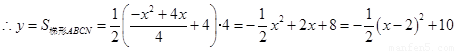
当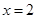 时,
时,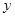 取最大值,最大值为10.······················ 8分
取最大值,最大值为10.······················ 8分
当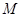 点为BC中点时,四边形
点为BC中点时,四边形 面积最大,最大面积是10;
面积最大,最大面积是10;
(3)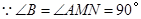
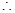 要使
要使 ,必须有
,必须有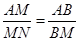
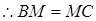 由(1)知
由(1)知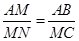
 当点
当点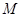 运动到
运动到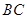 的中点时,
的中点时, .
.
此时,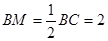
(1)要证三角形ABM和MCN相似,就需找出两组对应相等的角,已知了这两个三角形中一组对应角为直角,而∠BAM和∠NMC都是∠AMB的余角,因此这两个角也相等,据此可得出两三角形相似.
(2)根据(1)的相似三角形,可得出AB,BM,MC,NC的比例关系式,已知了AB=4,BM=x,可用BC和BM的长表示出CM,然后根据比例关系式求出CN的表达式.这样直角梯形的上下底和高都已得出,可根据梯形的面积公式得出关于y,x的函数关系式.然后可根据函数的性质得出y的最大值即四边形ABCN的面积的最大值,以及此时对应的x的值,也就可得出BM的长.
(3)已知了这两个三角形中相等的对应角是∠ABM和∠AMN,如果要想使Rt△ABM∽Rt△AMN,那么两组直角边就应该对应成比例,即AM:MN=AB:BM,根据(1)的相似三角形可得出AM:MN=AB:MC,因此BM=MC,M是BC的中点.即BM=2


科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
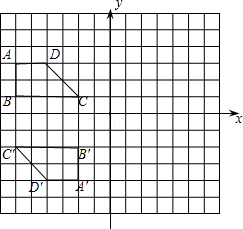 在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.
在直角坐标系中,两个全等的梯形ABCD和A′B′C′D′的位置如图所示,图中小正方形的边长为1个长度单位.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.
在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com