Question

操作：在△ABC中，AC=BC=2，∠C=90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点，如图3-1-13①②③是旋转三角板得到的图形中的3种情况，

由①②③研究：（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图①加以证明。

（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长；若不能，请说明理由）。

（3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB=1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图④加以证明。

 

 

 

Answer 1

解：（1）连接PC，因为△ABC是等腰直角三角形，P是AB的中点，所以CP=PB，CP⊥AB，∠ACP=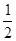∠ACP=45°，即∠ACP=∠B=45°，又因为∠DPC+∠CPE=∠BPE+∠CPE=90°，

 

所以∠DPC=∠BPE，即△PCD≌△PBE，所以PD=PE。…………………3分

（2）共有四种情况：①当点C与点E重合，即CE=0时，PE=PB，②当CE=2-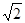时，此时PB=BE；③当CE=1时，此时PE=BE；④当E在CB的延长线上，且CE=2+时，此时PB=EB。…6分

（3）MD：ME=1：3，…………………7分

证明如下：过点M作MF⊥AC，MH⊥BC，垂足分别是F、H，所以MH∥AC，MF∥BC，即四边形CFMH是平行四边形，因为∠C=90°，所以□CFMH是矩形，即∠FMH=90°，MF=CH，因为，

 

而HB=MH，所以…………………9分，

 

因为∠DMF+∠DMH=∠DMH+∠EMH=90°，所以∠DMF=∠EMH，因为∠MFD=∠EMH=90°，所以△MDF∽△MEH，即…………………10分

 

解析:略