
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
【答案】C
【解析】试题分析:由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,
∵∠ABE+∠EBF=∠C′BF+∠EBF=90°
∴∠ABE=∠C′BF
在△BAE和△BC′F中,
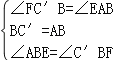
∴△BAE≌△BC′F(ASA),
∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,
△ABE和△BC′F的周长=2△ABE的周长=2×3=6.
故选:C.


科目:初中数学 来源: 题型:
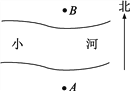
【题目】如图所示的A、B是两根呈南北方向排列的电线杆,A、B之间有一条小河,小刚想估测这两根电线杆之间的距离,于是小刚从A点开始向正西方向走了20步到达一棵大树C处,接着又向前走了20步到达D处,然后他左转90°直行,当他看到电线杆B、大树C和他自己现在所处的位置E恰在同一条直线上时,他从D位置走到E处恰好走了100步,利用上述数据,小刚测出了A、B两根电线杆之间的距离.
(1)请你根据上述的测量方法在原图上画出示意图;
(2)如果小刚一步大约60厘米,请你求A、B两根电线杆之间的距离并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.

(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O′A′BC′是矩形OABC绕B点逆时针旋转得到的.O′点恰好在x轴的正半轴上,O′C′交AB于点D.
(1)求点O′的坐标,并判断△O′DB的形状(要说明理由)
(2)求边C′O′所在直线的解析式.
(3)延长BA到M使AM=1,在(2)中求得的直线上是否存在点P,使得△POM是以线段OM为直角边的直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADF≌△CBE,且点E,B,D,F在一条直线上.试判断:
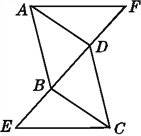
(1)AD与BC的位置关系(并加以说明);
(2)BF与DE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想知道湖中两个小亭A、B之间的距离,他在与小亭A、B位于同一水平面且东西走向的湖边小道![]() 上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道
上某一观测点M处,测得亭A在点M的北偏东30°方向, 亭B在点M的北偏东60°方向,当小明由点M沿小道![]() 向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.
向东走60米时,到达点N处,此时测得亭A恰好位于点N的正北方向,继续向东走30米时到达点Q处,此时亭B恰好位于点Q的正北方向,根据以上测量数据,请你帮助小明计算湖中两个小亭A、B之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com