
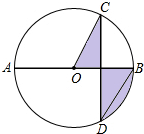
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{2π}{3}$ |
分析 根据垂径定理求得CE=ED=$\sqrt{3}$;然后由圆周角定理知∠COE=60°.然后通过解直角三角形求得线段OC,求出扇形COB面积,即可得出答案.
解答 解:∵AB是⊙O的直径,弦CD⊥AB,CD=2$\sqrt{3}$,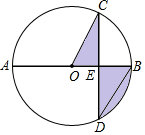
∴CE=$\frac{1}{2}$CD=$\sqrt{3}$,∠CEO=90°,
∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∴OC=$\frac{CE}{sin60°}$=2,
∴阴影部分的面积S=S扇形COB=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,
故选D.
点评 本题考查了垂径定理、解直角三角形,圆周角定理,扇形面积的计算等知识点,能知道阴影部分的面积=扇形COB的面积是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
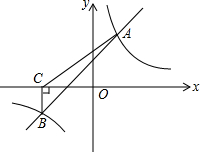 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.118×103 | B. | 1.118×1010 | C. | 1.118×1011 | D. | 1.118×1012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com