
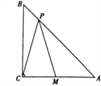
【题目】如图,在△ABC中,BC=AC=4,∠ACB =90°,点M是边AC的中点,点P是边AB上
的动点,则PM+PC的最小值为_______.
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
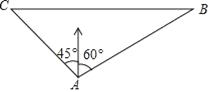
【题目】一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为_____海里/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解的范围是( )
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
A. 3<x<3.23 B. 3.23<x<3.24
C. 3.24<x<3.25 D. 3.25<x<3.26
查看答案和解析>>
科目:初中数学 来源: 题型:
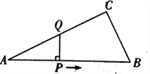
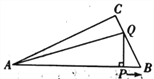
【题目】如图,△ABC中,∠ACB =90°,AB=1O, ![]() ,点P是斜边AB上一个动点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图像大致为 ( )
,点P是斜边AB上一个动点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图像大致为 ( )
A. 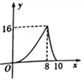 B.
B. 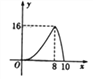 C.
C. 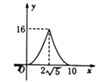 D.
D. 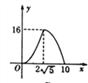
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.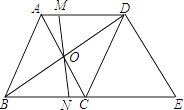
(1)请你判断OM与ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】医学研究发现一种新病毒的直径约为0.000043毫米,则0.000043用科学记数法表示()
A. 0.43×10-4B. 43x105C. 4.3x10-4D. 4.3×10-5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com