
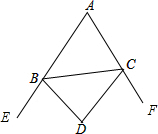
 如图,BD,CD分别平分△ABC的两个外角,若∠A=α,求∠BDC的度数.
如图,BD,CD分别平分△ABC的两个外角,若∠A=α,求∠BDC的度数.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
 一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )
一个正方形和四个全等的小正方形按图①②两种方式摆放,若把图②中未被小正方形覆盖部分(图②中的阴影部分)折成一个无盖的长方体盒子,则此长方体盒子的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
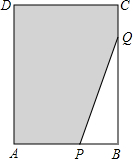 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:
 某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
某校部分团员参加社会公益活动,准备用每个6元的价格购进一批许愿瓶进行销售,并将所得利润捐给慈善机构,根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com