Question

【题目】Rt△ABC中，AB=AC，点D为BC中点．∠MDN=900，∠MDN绕点D旋转，DM、DN分别与边AB、AC交于E、F两点．下列结论

①(BE+CF)=BC，②，③AD·EF，④AD≥EF，⑤AD与EF可能互相平分，

其中正确结论的个数是（ ）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】

∵Rt△ABC中，AB=AC，点D为BC中点．∠MDN=900，

∴AD =DC，∠EAD=∠C=450，∠EDA=∠MDN－∠ADN =900－∠AND=∠FDC。

∴△EDA≌△FDC（ASA）。∴AE=CF。∴BE+CF=" BE+" AE=AB。

在Rt△ABC中，根据勾股定理，得AB=BC。∴(BE+CF)=BC。∴结论①正确。

设AB=AC=a，AE=b，则AF="BE=" a－b。

∴。

∴。∴结论②正确。

如图，过点E作EI⊥AD于点I，过点F作FG⊥AD于点G，过点F作FH⊥BC于点H，ADEF相交于点O。

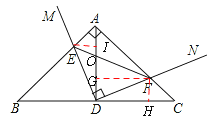
∵四边形GDHF是矩形，△AEI和△AGF是等腰直角三角形，

∴EO≥EI（EF⊥AD时取等于）=FH=GD，

OF≥GH（EF⊥AD时取等于）=AG。

∴EF=EO＋OF≥GD＋AG=AD。∴结论④错误。

∵△EDA≌△FDC，

∴。∴结论③错误。

又当EF是Rt△ABC中位线时，根据三角形中位线定理知AD与EF互相平分。

∴结论⑤正确。

综上所述，结论①②⑤正确。故选C。