练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知：a是-2的相反数，b是-2的倒数，则
    （1）a=2，b=-$\frac{1}{2}$；
    （2）求代数式a2b+ab的值．

    分析 （1）根据相反数和倒数定义得出即可；
    （2）先分解因式，再代入求出即可．

    解答 解：（1）∵a是-2的相反数，b是-2的倒数，
    ∴a=2，b=-$\frac{1}{2}$，
    故答案为：2，-$\frac{1}{2}$；

    （2）当a=2，b=-$\frac{1}{2}$时，a2b+ab=ab（a+1））=2×（-$\frac{1}{2}$）×（2+1）=-3．

    点评 本题考查了求代数式的值，相反数和倒数等知识点，能求出a、b的值是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．已知一组数据：2，2，2，2，2，则这组数据的方差为0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．计算：$\sqrt{4}$-（π-3）0-10sin30°-（-1）2017+${（\frac{1}{2}）}^{-2}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

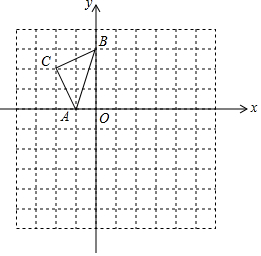    10．如图，在已知的平面直角坐标系中，△ABC的顶点都在正方形网格的格点上，若A，B两点的坐标分别是A（-1，0），B（0，3）．
    （1）将△ABC绕原点O顺时针旋转90°得到△A1B1C1，画出△A1B1C1；
    （2）以点O为位似中心，与△ABC位似的△A2B2C2满足A2B2：AB=2：1，请在网格内画出△A2B2C2，并直接填写△A2B2C2的面积为10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．雷达二维平面定位的主要原理是：测量目标的两个信息--距离和角度，目标的表示方法为（γ，α），其中，γ表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B，C处有目标出现，其中，目标A的位置表示为A（5，30°），目标B的位置表示为F（4，150°）．用这种方法表示目标C的位置，正确的是（　　）
    A．（-3，300°）B．（3，60°）C．（3，300°）D．（-3，60°）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．把抛物线y=-x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的顶点坐标为（-1，3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

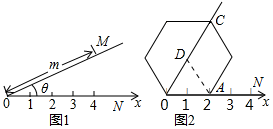    14．阅读理解：如图①所示，在平面内选一定点O，引一条有方向的射线ON，再选定一个单位长度，那么平面上任一点M的位置可由OM的长度m与∠MON的度数θ确定，有序数对（m，θ）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
    应用：在图②的极坐标系下，如果正六边形的边长为2，有一边OA在射线ON上，则正六边形的顶点C的极坐标应记为（　　）
    A．（4，60°）B．（4，45°）C．（2$\sqrt{2}$，60°）D．（2$\sqrt{2}$，50°）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．某中学对本校500名毕业生中考体育测试情况进行调查，根据男生及女生身体机能类选考坐位体前屈测试成绩整理，绘制成如下不完整的统计图（图①，图②）

    请根据统计图提供的信息，回答下列问题：
    （1）该校毕业生中男生有300人，女生有200人；
    （2）扇形统计图中a=12，b=62，并补全条形统计图；
    （3）求图①中“8分a%”所对应的扇形圆心角的度数；
    （4）若该校毕业生中随机抽取一名学生，则这名男生身体机能类选考坐位体前屈测试成绩为10分的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．为了参加我市“全民健身”系列活动，学校准备从甲、乙、丙三个舞蹈小组中选出一组参加比赛，已知这三个舞蹈小组的平均身高都是1.6m，方差分比为为S甲2=0.42，S乙2=0.29，S丙2=0.38，若选择身高较为整齐的队伍参加比赛，则应选择乙队．

    查看答案和解析>>

    同步练习册答案