
分析 利用十字相乘法把原式的左边进行因式分解,根据特殊角的三角函数值解答即可.
解答 解:∵2cos2α+(2-$\sqrt{3}$)cosα-$\sqrt{3}$=0,
∴(2cosα-$\sqrt{3}$)(cosα+1)=0,
∴cosα=$\frac{\sqrt{3}}{2}$或cosα=-1.
∵0<cosα<1,
∴cosα=$\frac{\sqrt{3}}{2}$,
∴锐角α=30°,
故答案为:2cosα-$\sqrt{3}$;cosα+1;$\frac{\sqrt{3}}{2}$;-1;0;1;$\frac{\sqrt{3}}{2}$;30°.
点评 本题考查的是特殊角的三角函数值、因式分解法解一元二次方程,熟记特殊角的三角函数值是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的内切圆,点D,E,F为切点.
如图,⊙O是△ABC的内切圆,点D,E,F为切点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
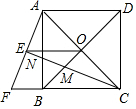 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个内角是60°的三角形 | |
| B. | 有两边相等且是轴对称图形的三角形 | |
| C. | 三边都相等的三角形 | |
| D. | 有一个角是60°且是轴对称图形的三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
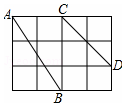 如图,在4×3正方形网格中,每个小正方形的边长都是1
如图,在4×3正方形网格中,每个小正方形的边长都是1查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 扩大10倍 | B. | 扩大100倍 | C. | 缩小10倍 | D. | 不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com