Question

如图，已知AB∥CD，分别写出下面四个图形中∠APC和∠PAB、∠PCD的数量关系，再请你从所写出的四个数量关系中任选一个，说明该数量关系的正确性．

数量关系：（1）______；（2）______；
（3）______；（4）______
选择：______　 说明理由：

Answer 1

解：（1）∠APC+∠PAB+∠PCD=360°，
（2）∠APC=∠PAB+∠PCD，
（3）∠APC+∠PAB=∠PCD，
（4）∠APC+∠PCD=∠PAB．
故答案为：∠APC+∠PAB+∠PCD=360°，∠APC=∠PAB+∠PCD，∠APC+∠PAB=∠PCD，∠APC+∠PCD=∠PAB．

（3）如图，理由如下：

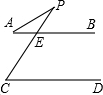
∵∠APC+∠PAB=∠PEB，
又已知AB∥CD，
∴∠PCD=∠PEB，
∴∠APC+∠PAB=∠PCD．
分析：（1）（2）过点P作两条平行线的平行线，由平行线的性质得出结论．（3）（4）由平行线的性质和三角形外角的性质得出结论．
点评：此题考查的知识点是评先的性质，关键是由平行线的性质和三角形外角性质得出．