
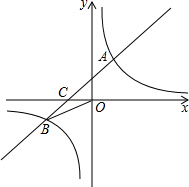
 已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=
已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=| k |
| x |
| k |
| x |
| k |
| x |
| k |
| x |
| 8 |
| x |
| 8 |
| x |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、三角形的内心是这个三角形三条边中垂线的交点 |
| B、矩形的对角线相等的逆命题是真命题 |
| C、一组数据2、9、7、5、4、8、5、3的中位数是5 |
| D、正六边形的外角和是720度 |
查看答案和解析>>
科目:初中数学 来源: 题型:
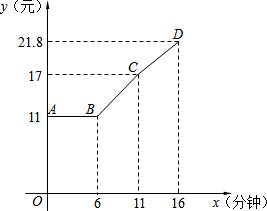 某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).查看答案和解析>>
科目:初中数学 来源: 题型:
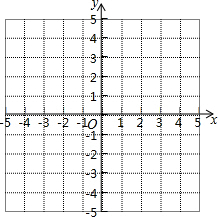 已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
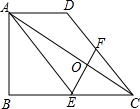 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com