
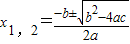 )
) ,
, )+(2-
)+(2- )=4.
)=4. )•(2-
)•(2- )=k+1.
)=k+1. =4,
=4, =k+1(以下同解法一).
=k+1(以下同解法一). ,x1x2=
,x1x2= ,本题运用解法二更简便.
,本题运用解法二更简便. 

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷27(沈瑜瑛)(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《反比例函数》(02)(解析版) 题型:选择题




查看答案和解析>>
科目:初中数学 来源:2009年广东省茂名市中考数学试卷(解析版) 题型:解答题
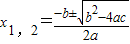 )
)查看答案和解析>>
科目:初中数学 来源:2009年广东省茂名市中考数学试卷(解析版) 题型:选择题
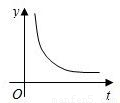
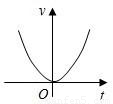
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com