
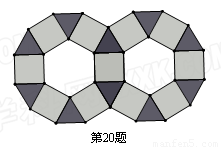
如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)
.解:(1)∵图案中正三角形的边长为2,∴高为 .(1分)
.(1分)
∴正三角形的面积为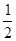 ×2×
×2× =
=  .
(2分)
.
(2分)
(2)∵图中共有11个正方形, ∴图中正方形的面积和为11×(2×2)=44. (3分)
∵图中共有2个正六边形,∴图中正六边形的面积和为2×(6×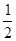 ×2×
×2×  )=12
)=12 .(4分)∵图中共有10个正三角形,∴图中正三角形的面积和为10
.(4分)∵图中共有10个正三角形,∴图中正三角形的面积和为10  .
.
∵镶嵌图形的总面积为44+10  +12
+12 =44+22
=44+22  (5分)≈81.4,
(5分)≈81.4,
∴点O落在镶嵌图案中正方形区域的概率为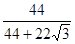 (7分)≈0.54.(8分)
(7分)≈0.54.(8分)
答:点O落在镶嵌图案中正方形区域的概率为0.54.(“≈”写为“=”不扣分)
【解析】略


科目:初中数学 来源: 题型:
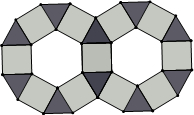 镶嵌图案.
镶嵌图案.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•锦江区一模)如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为
(2012•锦江区一模)如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
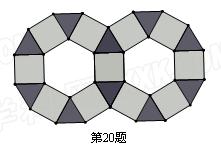
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川乐山卷)数学 题型:解答题
如图,某商标 是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com