③④
分析:若y
1=y
2,记M=y
1=y
2.首先求得抛物线与直线的交点坐标,利用图象可得当x<-1时,利用函数图象可以得出y
2>y
1;当-1<x<0时,y
1>y
2;当x>0时,利用函数图象可以得出y
2>y
1;然后根据当x任取一值时,x对应的函数值分别为y
1、y
2.若y
1≠y
2,取y
1、y
2中的较小值记为M;即可求得答案.
解答:∵当y
1=y
2时,即-2x
2+2=2x+2时,
解得:x=0或x=-1,
∴当x<-1时,利用函数图象可以得出y
2>y
1;当-1<x<0时,y
1>y
2;当x>0时,利用函数图象可以得出y
2>y
1;
∴①错误;
∵抛物线y
1=-2x
2+2,直线y
2=2x+2,当x任取一值时,x对应的函数值分别为y
1、y
2.若y
1≠y
2,取y
1、y
2中的较小值记为M;
∴当x<0时,根据函数图象可以得出x值越大,M值越大;
∴②错误;
∵抛物线y
1=-2x
2+2,直线y
2=2x+2,与y轴交点坐标为:(0,2),当x=0时,M=2,抛物线y
1=-2x
2+2,最大值为2,故M大于2的x值不存在;
∴使得M大于2的x值不存在,
∴③正确;
∵如图:当-1<x<0时,y
1>y
2;
∴使得M=1时,y
2=2x+2=1,解得:x=-

;
当x>0时,y
2>y
1,
使得M=1时,即y
1=-2x
2+2=1,解得:x
1=

,x
2=-

(舍去),
∴使得M=1的x值是-

或

.
∴④正确;
故答案为:③④.
点评:此题主要考查了二次函数与一次函数综合应用.注意掌握函数增减性是解题关键,注意数形结合思想与方程思想的应用.

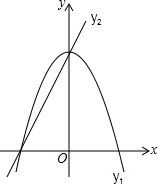 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: 或
或 .
. ;
; ,x2=-
,x2=- (舍去),
(舍去), 或
或 .
.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
 (2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
(2012•义乌市)如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.那么使得M=1的x值为
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.那么使得M=1的x值为
 如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:
如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断: