
 甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米.
甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地100千米. 分析 当x=0时,y=300,故此可得到AB两地的距离为300,3小时后两车相遇,从而可求得两车的速度之和,然后依据5小时后两车的距离最大,可知甲车到达B地用5小时,从而可乙车的速度,由图象可知甲车到达B地的时间,从而知道乙车5小时行驶的路程,继而得出答案.
解答 解:由图象可得:当x=0时,y=300,
∴AB=300千米.
∴甲车的速度=300÷5=60千米/小时,
又∵300÷3=100千米/小时,
∴乙车的速度=100-60=40千米/小时.
由图象可知当x=5时,甲车到达B地,
此时乙车行驶的路程为5×40=200(千米),
∴乙车距离A地100千米,
故答案为:100.
点评 本题以行程问题为背景的函数图象的应用,解决问题的关键是根据函数图象理解题意,求得两车的速度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
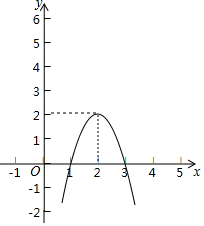 如图,二次函数y=-2(x-2)2+2的图象.
如图,二次函数y=-2(x-2)2+2的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抽取件数(件) | 50 | 100 | 200 | 500 | 800 | 1000 |
| 合格频数 | 47 | 93 | 189 | 489 | 760 | 950 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com