
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
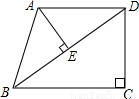
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
(1)证明见解析;(2)15.
【解析】
试题分析:(1)由等腰三角形的性质可知∠ABD=∠ADB,由AD∥BC可知,∠ADB=∠DBC,由此可得∠ABD=∠DBC,又∵∠AEB=∠C=90°,利用“AA”可证△ABE∽△DBC;(2)由等腰三角形的性质可知,BD=2BE,根据△ABE∽△DBC,利用相似比求BE,在Rt△ABE中,利用勾股定理求AE.
试题解析:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.
∵AD∥BC,∴∠ADB=∠DBC. ∴∠ABD=∠DBC.
∵AE⊥BD,∴∠AEB=∠C=90°。∴△ABE∽△DBC.
(2)∵AB=AD,又AE⊥BD,∴BE=DE. ∴BD=2BE.
由△ABE∽△DBC,得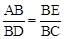 .
.
∵AB=AD=25,BC=32,∴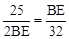 ,解得BE=20.
,解得BE=20.
∴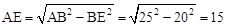 .
.
考点:1.直角梯形的性质;2.等腰三角形的性质;3.平行的性质;4.相似三角形的判定和性质;5.勾股定理.


科目:初中数学 来源: 题型:
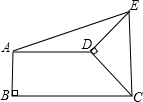 DC逆时针旋转90°至DE,连接AE、CE.
DC逆时针旋转90°至DE,连接AE、CE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 | 7 |
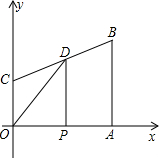 函数关系式,并指出自变量t的取值范围.
函数关系式,并指出自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
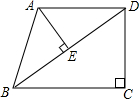 (2012•铁岭)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
(2012•铁岭)已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知:在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E
如图,已知:在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com