
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.
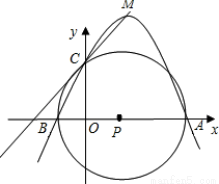
(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
(1)y=-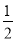 x2+
x2+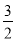 x+2,(2)
x+2,(2)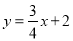 .(3)MC与⊙P的位置关系是相切.证明见解析.
.(3)MC与⊙P的位置关系是相切.证明见解析.
【解析】
试题分析:(1)求出半径,根据勾股定理求出C的坐标,设经过A、B、C三点抛物线解析式是y=a(x-4)(x+1),把C(0,2)代入求出a即可;
(2)求出M的坐标,设直线MC对应函数表达式是y=kx+b,把C(0,2),M(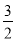 ,
,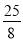 )代入得到方程组,求出方程组的解即可;
)代入得到方程组,求出方程组的解即可;
(3)根据点的坐标和勾股定理分别求出PC、DC、PD的平方,根据勾股定理的逆定理得出∠PCD=90°,即可求出答案.
试题解析:(1)连接PC,
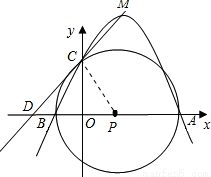
∵A(4,0),B(-1,0),
∴AB=5,半径PC=PB=PA=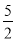 ,
,
∴OP=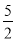 -1=
-1=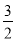 ,
,
在△CPO中,由勾股定理得:OC=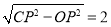
∴C(0,2),
设经过A、B、C三点抛物线解析式是y=a(x-4)(x+1),
把C(0,2)代入得:2=a(0-4)(0+1),
∴a=-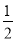 ,
,
∴y=-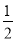 (x-4)(x+1)=-
(x-4)(x+1)=-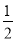 x2+
x2+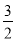 x+2,
x+2,
(2)y=-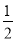 x2+
x2+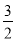 x+2=-
x+2=-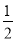 (x-
(x-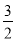 )2+
)2+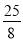 ,
,
M(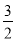 ,
,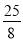 ),
),
设直线MC对应函数表达式是y=kx+b,
把C(0,2),M(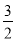 ,
,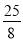 )代入得:
)代入得:

解得: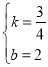 ,
,
∴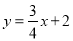 .
.
(3)MC与⊙P的位置关系是相切.
证明:设直线MC交x轴于D,
当y=0时,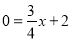 ,
,
∴x=-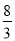 ,OD=
,OD=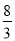 ,
,
∴D(-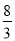 ,0),
,0),
在△COD中,由勾股定理得:CD2=22+(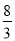 )2=
)2=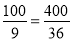 ,
,
PC2=(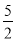 )2=
)2=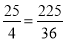 ,
,
PD2=(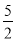 +
+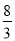 -1)2=
-1)2=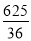 ,
,
∴CD2+PC2=PD2,
∴∠PCD=90°,
∴PC⊥DC,
∵PC为半径,
∴MC与⊙P的位置关系是相切.
考点:二次函数综合题


科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,AB=15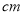 ,BC=10
,BC=10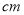 ,点P沿AB边从点A开始向B点以
,点P沿AB边从点A开始向B点以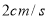 的速度移动,点Q沿DA边从点D开始向点A以
的速度移动,点Q沿DA边从点D开始向点A以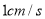 的速度移动。若P、 Q同时出发,用t(秒)表示移动时间。
的速度移动。若P、 Q同时出发,用t(秒)表示移动时间。

(1)问:当t=5时,求Δ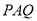 的面积是多少?
的面积是多少?
(2)当t为何值时,Δ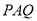 为等腰直角三角形?
为等腰直角三角形?
(3)当t为何值时,以点P、A、Q为顶点的 Δ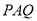 与Δ
与Δ 相似?
相似?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省仁寿县联谊学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在ΔABC中,DE//BC,AQ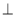 BC于Q,交DE于P,AD=3,BD=2,则
BC于Q,交DE于P,AD=3,BD=2,则 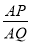 等于( )
等于( )

A.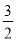 B.
B.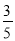 C.
C.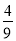 D.
D.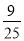
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:解答题
如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
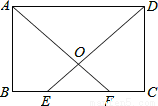
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省九年级上学期第二次月考数学试卷(解析版) 题型:填空题
小明从图所示的二次函数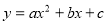 的图象中,观察得出了下面五条信息:①
的图象中,观察得出了下面五条信息:①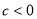 ;②
;②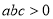 ;③
;③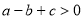 ;④
;④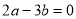 ;⑤
;⑤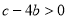 ,你认为其中正确信息有 。
,你认为其中正确信息有 。
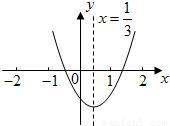
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月月考数学试卷(解析版) 题型:解答题
为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省咸宁市中考模拟考试数学试卷(解析版) 题型:选择题
函数y= 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A.x≠4 B.x>4 C.x≥4 D.x≤4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com