Question

已知四边形ABCD是正方形，O为正方形对角线的交点，一动点P从B开始，沿射线BC运动，连结DP，作CN⊥DP于点M，且交直线AB于点N，连结OP，ON。（当P在线段BC上时，如图1：当P在BC的延长线上时，如图2）

 （1）请从图1，图2中任选一图证明下面结论：

        ①BN=CP：    ②OP=ON，且OP⊥ON

  (2)  设AB=4，BP=x，试确定以O、P、B、N为顶点的四边形的面积y与x的函数关系。

 

 

 

Answer 1

【答案】

（1）证明：如图1，

①∵四边形ABCD是正方形，

∴OC=OB，DC=BC，∠DCB=∠CBA=90°，∠OCB=∠OBA=45°，∠DOC=90°，DC∥AB。

∵DP⊥CN，∴∠CMD=∠DOC=90°。

∴∠BCN+∠CPD=90°，∠PCN+∠DCN=90°。∴∠CPD=∠CNB。

∵DC∥AB，∴∠DCN=∠CNB=∠CPD。

∵在△DCP和△CBN中，∠DCP=∠CBN，∠CPD=∠BNC，DC=BC，

∴△DCP≌△CBN（AAS）。∴CP=BN。

②∵在△OBN和△OCP中，OB=OC，∠OCP=∠OBN， CP=BN ，

∴△OBN≌△OCP（SAS）。∴ON=OP，∠BON=∠COP。

∴∠BON+∠BOP=∠COP+∠BOP，即∠NOP=∠BOC=90°。

∴ON⊥OP。

（2）解：∵AB=4，四边形ABCD是正方形，∴O到BC边的距离是2。

图1中，，

图2中，。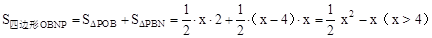

∴以O、P、B、N为顶点的四边形的面积y与x的函数关系是：

 。

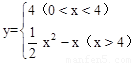【解析】正方形的性质，三角形外角性质，全等三角形的判定和性质，两线垂直的判定，多边形的面积的分解，函数解析式的确定，分段函数，点到直线的距离。

【分析】（1）对于图1，证明线段相等，一般情况下找全等。根据BN，CP的分布情况 可以观察△CNB和△DPC，然后证明两三角形全等。也可以观察△CAN和△DBP，证明AN=BP，从而有BN=CP。

对于图2，证明如下：

①∵ABCD为正方形，AC，BD为对角线，∴∠DCP=90º。

             ∵CM⊥DP， ∴∠PCM=∠PDC。∴∠PDB=∠CAN。

             又∵∠DPB=∠ANC，BD=AC，∴△PDB≌△NCA（ASA）。

             ∴PB=AN，DP=CN。∴CP=BN。

             ②∵∠PDB=∠CAN，OD=OC， CP=BN，∴△PDO≌△NCO（SAS）。

             ∴OP=ON，∠DOP=∠CON。

             ∵∠DOC=90º，∴∠PON=∠NOC+POC=∠DOP+∠POC=∠DOC=90º。∴OP⊥ON。

（2）求以O、P、B、N为顶点的四边形的面积，则要把四边形分解为两个三角形去解决问题。图1中，S_{四边形OPBN}=S_△OBN+S_△BOP，，；图2中，S_{四边形OBNP}=S_△POB+S_△PBN，代入求出即可。