
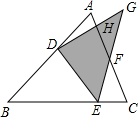
 如图,将△ABC沿虚线DE折叠,得到一个七边形ADECFGH.若七边形和原三角形的面积比为2:3,且折叠后重叠部分面积为4,则原△ABC的面积为________.
如图,将△ABC沿虚线DE折叠,得到一个七边形ADECFGH.若七边形和原三角形的面积比为2:3,且折叠后重叠部分面积为4,则原△ABC的面积为________.科目:初中数学 来源:2010年四川省内江市高中阶段教育学校招生考试数学试卷 题型:013
学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚BC剪下△ABC,展开即可得到一个五角星.如果想得到一个正五角星(如图④),那么在图③中剪下△ABC时,应使∠ABC的度数为

126°
108°
100°
90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com