
解:(1)∵点A的坐标为(

,2),AB∥x轴,
∴B点纵坐标为2,
又点B在函数
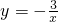
(x<0)的图象上,
∴当y=2时,x=-1.5,∴B(-1.5,2),
∵BC∥y轴,
∴C点横坐标为-1.5,
又点C在函数

(x<0)的图象上,
∴当x=-1.5时,y=-4,∴C(-1.5,-4).
∵AD⊥y轴,
∴D(0.5,-4).
(2)若点A在函数

(x>0)上移动,矩形ABCD的面积不变.理由如下:
如图,设AB、CD与y轴分别交于F、G,BC、AD与x轴分别交于E、H,设A(a,

),则B(-3a,

),C(-3a,-

),D(a,-

).
∵矩形ABCD的面积=矩形AFOH的面积+矩形BFOE的面积+矩形CEOG的面积+矩
形DHOG的面积=1+3+6+2=12.
(3)设A(t,
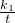
),则B(
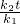
,
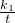
),C(
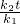
,
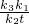
),D(t,
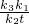
),
又∵点D在y=
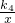
的图象上,
t•
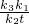
=k
4,
∴k
1k
3=k
2k
4.
分析:(1)根据平行于x轴上的两点其纵坐标相同,平行于y轴上的两点其横坐标相同,以及点在函数的图象上即点的坐标满足函数的解析式,即可求出点D的坐标;
(2)设A(a,

),用含a的代数式分别表示B、C、D三点的坐标,然后根据反比例函数比例系数k的几何意义,可知矩形ABCD的面积是一个固定的常数,因而面积不变;
(3)设A(t,
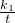
),则可用含t的代数式分别表示B、C、D三点的坐标,然后根据点D也在y=
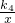
的图象上,所以点D的坐标满足此函数的解析式,从而得出k
1、k
2、k
3、k
4满足的数量关系式.
点评:本题主要考查了平行于x轴上的两点与平行于y轴上的两点的坐标特征,反比例函数比例系数k的几何意义等知识,难度较大.

 (x>0)的图象上,点B在函数
(x>0)的图象上,点B在函数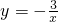 (x<0)的
(x<0)的 图象上,点C在函数
图象上,点C在函数 (x<0)的图象上,且AB∥x轴,BC∥y轴,四边形ABCD是以AB、BC为一组邻边的矩形.
(x<0)的图象上,且AB∥x轴,BC∥y轴,四边形ABCD是以AB、BC为一组邻边的矩形. ,2),求点D的坐标;
,2),求点D的坐标; (x>0)上移动,矩形ABCD的面积是否变化?如果不变,求出其面积;
(x>0)上移动,矩形ABCD的面积是否变化?如果不变,求出其面积;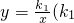 >0,x>0),
>0,x>0),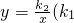 <0,x<0),
<0,x<0), >0,x<0),
>0,x<0), <0,x>0)上,请直接写出k1、k2、k3、k4满足的数量关系式.
<0,x>0)上,请直接写出k1、k2、k3、k4满足的数量关系式. 解:(1)∵点A的坐标为(
解:(1)∵点A的坐标为( ,2),AB∥x轴,
,2),AB∥x轴,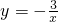 (x<0)的图象上,
(x<0)的图象上, (x<0)的图象上,
(x<0)的图象上, (x>0)上移动,矩形ABCD的面积不变.理由如下:
(x>0)上移动,矩形ABCD的面积不变.理由如下: ),则B(-3a,
),则B(-3a, ),C(-3a,-
),C(-3a,- ),D(a,-
),D(a,- ).
).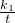 ),则B(
),则B(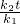 ,
,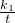 ),C(
),C(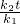 ,
,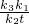 ),D(t,
),D(t,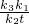 ),
),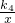 的图象上,
的图象上,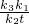 =k4,
=k4, ),用含a的代数式分别表示B、C、D三点的坐标,然后根据反比例函数比例系数k的几何意义,可知矩形ABCD的面积是一个固定的常数,因而面积不变;
),用含a的代数式分别表示B、C、D三点的坐标,然后根据反比例函数比例系数k的几何意义,可知矩形ABCD的面积是一个固定的常数,因而面积不变;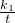 ),则可用含t的代数式分别表示B、C、D三点的坐标,然后根据点D也在y=
),则可用含t的代数式分别表示B、C、D三点的坐标,然后根据点D也在y=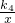 的图象上,所以点D的坐标满足此函数的解析式,从而得出k1、k2、k3、k4满足的数量关系式.
的图象上,所以点D的坐标满足此函数的解析式,从而得出k1、k2、k3、k4满足的数量关系式.

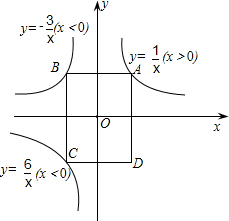 图象上,点C在函数y=
图象上,点C在函数y= 如图,已知点A在反比例函数y=
如图,已知点A在反比例函数y= 如图,已知点B在反比例函数y=
如图,已知点B在反比例函数y= (x>0)的图象上,点B在函数
(x>0)的图象上,点B在函数 (x<0)的图象上,点C在函数
(x<0)的图象上,点C在函数 (x<0)的图象上,且AB∥x轴,BC∥y轴,四边形ABCD是以AB、BC为一组邻边的矩形.
(x<0)的图象上,且AB∥x轴,BC∥y轴,四边形ABCD是以AB、BC为一组邻边的矩形. ,2),求点D的坐标;
,2),求点D的坐标; (x>0)上移动,矩形ABCD的面积是否变化?如果不变,求出其面积;
(x>0)上移动,矩形ABCD的面积是否变化?如果不变,求出其面积; >0,x>0),
>0,x>0), <0,x<0),
<0,x<0), >0,x<0),
>0,x<0), <0,x>0)上,请直接写出k1、k2、k3、k4满足的数量关系式.
<0,x>0)上,请直接写出k1、k2、k3、k4满足的数量关系式.