
【题目】如图,直线![]() 交x轴于点A(8,0),直线
交x轴于点A(8,0),直线![]() 经过点A,交y轴于点B,点P是直线
经过点A,交y轴于点B,点P是直线![]() 上的一个动点,过点P作x轴的垂线,过点B作y轴的垂线,两条垂线交于点D,连接PB,设点P的横坐标为m.
上的一个动点,过点P作x轴的垂线,过点B作y轴的垂线,两条垂线交于点D,连接PB,设点P的横坐标为m.
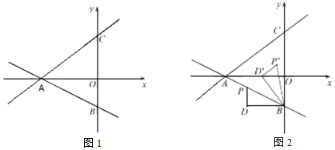
(1)若点P的横坐标为m,则PD的长度为 (用含m的式子表示);
(2)如图1,已知点Q是直线![]() 上的一个动点,点E是x轴上的一个动点,是否存在以A,B,E,Q为顶点的平行四边形,若存在,求出E的坐标;若不存在,说明理由;
上的一个动点,点E是x轴上的一个动点,是否存在以A,B,E,Q为顶点的平行四边形,若存在,求出E的坐标;若不存在,说明理由;
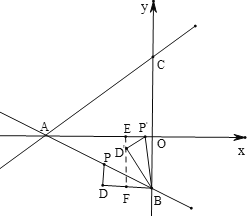
(3)如图2,将△BPD绕点B旋转,得到△BD′P′,且旋转角∠PBP′=∠OCA,当点P的对应点P′落在坐标轴上时,请直接写出点P的坐标.
【答案】(1)![]() ;(2)存在,点E坐标为(
;(2)存在,点E坐标为(![]() ,0)或(
,0)或(![]() ,0);(3)P′坐标为(-
,0);(3)P′坐标为(-![]() ,0)或(8,0).
,0)或(8,0).
【解析】
(1)直线解析式可得B点坐标,根据P横坐标可求出点P的纵坐标,根据两点间距离公式即可求出PD的长度;(2)分AB为边且点E在点A右侧、左侧和AB为对角线三种情况讨论,分别求出E点坐标即可;(3)①当m<0时,过D′作EF⊥BD,交x轴于E,BD与F,可得P(m,![]() m-4),D(m,-4),可用m表示PD、BD的长,利用勾股定理可得出BP的长,根据A、B、C三点坐标可求出AC、OC、OB的长,利用旋转的性质可得∠PBP′=∠OCA=∠DBD′,即可证明△OCA∽△FBD′,根据相似三角形的性质可得FB=OE的长,利用同角的余角相等的性质可得∠ED′P′=∠FBD′=∠OCA,即可证明△D′EP′∽△COA,可得EP′的长,即可求出OP′的长,利用勾股定理列方程即可求出m的值,可求出OP′的长,即可得P′坐标;②当m>0时,同①可得△OCA∽△FBD′,△D′EP′∽△COA,即可求出OP′的长,可得P′坐标.综上即可得答案.
m-4),D(m,-4),可用m表示PD、BD的长,利用勾股定理可得出BP的长,根据A、B、C三点坐标可求出AC、OC、OB的长,利用旋转的性质可得∠PBP′=∠OCA=∠DBD′,即可证明△OCA∽△FBD′,根据相似三角形的性质可得FB=OE的长,利用同角的余角相等的性质可得∠ED′P′=∠FBD′=∠OCA,即可证明△D′EP′∽△COA,可得EP′的长,即可求出OP′的长,利用勾股定理列方程即可求出m的值,可求出OP′的长,即可得P′坐标;②当m>0时,同①可得△OCA∽△FBD′,△D′EP′∽△COA,即可求出OP′的长,可得P′坐标.综上即可得答案.
(1)∵直线![]() 经过点A,交y轴于点B,
经过点A,交y轴于点B,
∴B坐标为(0,-4),
∵点P是直线![]() 上的一个动点,点P的横坐标为m,
上的一个动点,点P的横坐标为m,
∴点P的纵坐标为![]() m-4,
m-4,
∵PD⊥BD,
∴PD=![]() =
=![]() ,
,
故答案为:![]()
(2)∵直线AB的解析式为:![]() ,
,
∴B(0,-4),
∵直线![]() 交x轴于点A(8,0),
交x轴于点A(8,0),
∴![]() ×(-8)+n=0,
×(-8)+n=0,
解得:n=6,
∴直线AC的解析式为y=![]() x+6,
x+6,
∴C(0,6),
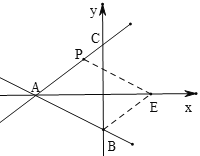
①如图,当AB为边,且点E在A点右侧时,
∵四边形ABEP是平四边形,
∴BE//AP,
∵直线AP的解析式为y=![]() x+6,B(0,-4)
x+6,B(0,-4)
∴直线BE的解析式为:y=![]() x-4,
x-4,
令y=0,得:![]() x-4=0,
x-4=0,
解得:x=![]() ,
,
∴E(![]() ,0),
,0),
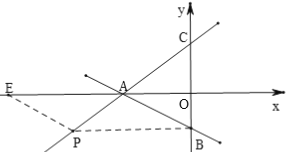
②当AB为边,点E在点A左侧时,
∵四边形EAPB是平行四边形,
∴PE//AB,PB//AE,
∵B(0,-4),
∴把y=-4代入y=![]() x+6得:x=
x+6得:x=![]() ,
,
∴P点坐标为(![]() ,-4),
,-4),
设直线PE的解析式为y=![]() x+b,
x+b,
把P点坐标代入得:![]() ×(
×(![]() )+b=-4,
)+b=-4,
解得:b=![]() ,
,
∴直线PE的解析式为y=![]() x
x![]() ,
,
令y=0得:![]() x
x![]() =0,
=0,
解得:x=![]() ,
,
∴点E坐标为(![]() ,0).
,0).
③当AB为对角线时,
∵四边形APBE是平行四边形,
∴BE//AP,
同①可得E点坐标为(![]() ,0),
,0),
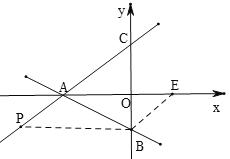
综上所述:存在以A,B,E,Q为顶点的平行四边形,点E坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
(3)①如图,当m<0时,过D′作EF⊥BD,交x轴于E,BD与F,
∵A(-8,0),C(0,6),B(0,-4),
∴AC=10,OC=6,OB=4,
∵点P在直线y=![]() x-4图象上,BD//y轴,BD⊥PD,
x-4图象上,BD//y轴,BD⊥PD,
∴P(m,![]() m-4),D(m,-4),
m-4),D(m,-4),
∴DP=![]() m-4-(-4)=
m-4-(-4)=![]() m,BD=-m,
m,BD=-m,
∴PB2=PD2+BD2=![]() m2,
m2,
∵旋转角∠PBP′=∠OCA=∠DBD′,∠D′FB=∠OCA,
∴△OCA∽△FBD′,
∴![]() ,
,
∵△BPD绕点B旋转,得到△BD′P′,
∴P′B=PB,BD′=BD=-m,D′P′=DP=![]() m,∠P′D′B=∠PDB=90°,
m,∠P′D′B=∠PDB=90°,
∴![]() ,
,
解得:FB=![]() m,
m,
∴OE=FB=![]() m,
m,
∵∠FD′B+∠FBD′=90°,∠ED′P′+∠FD′B=90°,
∴∠ED′P′=∠FBD′=∠OCA,
又∵∠D′EP′=∠AOC=90°,
∴△D′EP′∽△COA,
∴![]() ,即
,即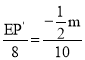 ,
,
解得:EP′=![]() ,
,
∴P′O=OE-EP=![]() m-(
m-(![]() )=-
)=-![]() m,
m,
∴P′B2=P′O2+OB2,即![]() m2=(-
m2=(-![]() m)2+42,
m)2+42,
解得:m=-![]() 或m=
或m=![]() ,
,
∵m<0,
∴m=-![]() ,
,
∴OP′=-![]() m=
m=![]() ,
,
∴P′坐标为(-![]() ,0),
,0),
②如图,当m>0时,过D′作EF⊥BD,交x轴于E,BD于F,P(m,![]() m-4),D(m,-4),
m-4),D(m,-4),
∴P′D′=PD=![]() m,BD′=BD=m,P′B2=PB2=
m,BD′=BD=m,P′B2=PB2=![]() m2,
m2,
同①可得△OCA∽△FBD′,△D′EP′∽△COA,
∴BF=OE=![]() m,EP′=
m,EP′=![]() m,
m,
∴P′O=OE+EP′=![]() m+
m+![]() m=m,
m=m,
∴P′O2+OB2=P′B2,即m2+42=![]() m2,
m2,
解得:m=±8,
∵m>0,
∴m=8,
∴OP′=m=8,
∴P′坐标为(8,0).
综上所述:P′坐标为(-![]() ,0)或(8,0).
,0)或(8,0).


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,﹣4).
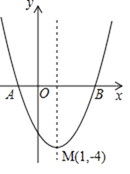
(1)求出图象与x轴的交点A、B的坐标;
(2)在y轴上存在一点Q,使得△QMB周长最小,求出Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
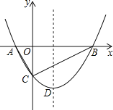
(1)求抛物线的解析式和顶点![]() 的坐标;
的坐标;
(2)判断![]() 的形状,证明你的结论;
的形状,证明你的结论;
(3)点![]() 是
是![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的周长最小时,求
的周长最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点的年游客量y(万人)是门票价格x(元)的一次函数,其函数图像如下图.

(1)求y关于x的函数解析式;
(2)经过景点工作人员统计发现:每卖出一张门票所需成本为20元.那么要想获得年利润11500万元,且门票价格不得高于230元,该年的门票价格应该定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,商场决定采取适当的降价措施.经调查发现,每件该商品每降价1元,商场平均每天可多售出10件.设每件商品降价x元.据此规律,请回答:
(1)降价后每件商品盈利 元,商场日销售量增加 件 (用含x的代数式表示);
(2)在上述条件不变的情况下,求每件商品降价多少元时,商场日盈利最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
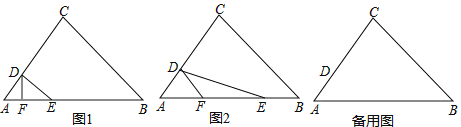
【题目】在△ABC中,AC=25,AB=35,tanA=![]() ,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
,点D为边AC上一点,且AD=5,点E、F分别为边AB上的动点(点F在点E的左边),且∠EDF=∠A.设AE=x,AF=y.
(1)如图1,当DF⊥AB时,求AE的长;
(2)如图2,当点E、F在边AB上时,求y关于x的函数关系式,并写出函数的定义域;
(3)联结CE,当△DEC和△ADF相似时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com