解:(1)设p=kx+b(k≠0)由题得:
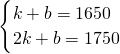
,
解得:
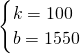
,
∴p=100x+1550;
(2)设日销售额为W元,则
W=pq=(100x+1550)(-0.2x+5)=-20x
2+190x+7750,
∵-20<0,
∴当x=-

=

=4.75时,W最大,
但x为整数,
∴当x=5时,W
最大=8200,
此时q=-0.2×5+5=4,p=100×5+1550=2050,
∴第5天的销售额最大,最大值为8200元,当天价格为4元/千克,销售量2050千克;
(3)由题意,一瓶橘子罐头含果肉500×
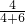
÷1000=0.2(千克),
则 7×4(1-8a%)×2050(1+5a%)+
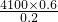
×3.5(1+20a%)=143500,
设a%=t,则原方程整理变为:160t
2-48t+3=0,
解得:t=
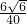
,
则t
1≈0.09,t
2≈0.21,
∴a
1≈9,a
2≈21>10(舍去).
∴a的整数值为9.
分析:(1)设p=kx+b,根据第一天销售量就为1650千克,第二天销售量为1750千克,可求出价格p与天数x之间的函数关系式;
(2)根据(1)所得的关系式及销售量q(千克)与天数x(天)之间满足q=100x+1550,可表示出销售收入的二次函数表达式,求最值即可得出答案;
(3)根据第二周价格与销量的变化,第二周该果园基地销售总额共计143500元可得出关于a的方程,解出即可得出答案.
点评:此题考查了二次函数的应用,涉及了待定系数法求函数解析式及公式法求二次函数最值的知识,综合性较强,难度较大,解答本题的关键是认真审题,将实际问题转化为数学问题解答.

 ,
, ,
, )
)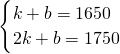 ,
,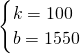 ,
, =
= =4.75时,W最大,
=4.75时,W最大,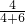 ÷1000=0.2(千克),
÷1000=0.2(千克),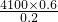 ×3.5(1+20a%)=143500,
×3.5(1+20a%)=143500,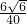 ,
,

 期末集结号系列答案
期末集结号系列答案