
分析:根据题意画出相应的图形,如图所示,由AD与BC垂直,得到三角形ABD与三角形ACD都为直角三角形,可得出一对直角相等,在直角三角形ABD中,根据直角三角形的两锐角互余得到一对角互余,再由直角三角形ABC的两锐角互余得到另一对角互余,根据同角的余角相等可得出一对角相等,根据两对对应角相等的两三角形相似可得出三角形ABD与三角形ACD相似,由相似得比例列出比例式,设AD为x,在直角三角形ABD中,由AB及AD,利用勾股定理表示出BD,将DC,BD及AD代入比例式中,列出关于x的方程,求出方程的解得出x的值,即为AD的长.
解答:根据题意画出相应的图形,如图所示:
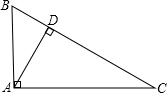
∵AD⊥BC,∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
又∠BAC=90°,∴∠B+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△CAD,
∴AD
2=BD•DC,
设AD=x,在Rt△ABD中,AD=x,AB=2

,
根据勾股定理得:BD=
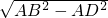
=
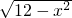
,
又BD=4,
∴x
2=4
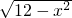
,
两边平方得:x
4=16(12-x
2),即x
4+16x
2-192=0,
因式分解得:(x
2+24)(x
2-8)=0,
可得:x
2=-24(舍去),x
2=8,
解得:x=2

,或x=-2

(舍去),
则CD=2

.
故答案为:2

点评:此题考查了相似三角形的判定与性质,勾股定理,以及垂直的定义,利用了转化的思想,熟练掌握相似三角形的判定与性质是解本题的关键.

 ,DC=4,则AD的长为________.
,DC=4,则AD的长为________.

 ,
,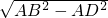 =
=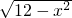 ,
,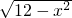 ,
, ,或x=-2
,或x=-2 (舍去),
(舍去), .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.