
 如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角(∠AOB)为120°,BC的长为2$\sqrt{3}$,则三角板和量角器重叠部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.
如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角(∠AOB)为120°,BC的长为2$\sqrt{3}$,则三角板和量角器重叠部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$. 分析 根据题意和锐角三角函数求出OB、OC的长,根据扇形面积公式和三角形面积公式计算即可.
解答 解:∵∠AOB=120°,∴∠BOC=60°
∵∠OCB=90°,BC=2$\sqrt{3}$,
∴OC=$\frac{2\sqrt{3}}{tan60°}$=2,OB=4,
∴重叠部分的面积=$\frac{120×π×{4}^{2}}{360}$+$\frac{1}{2}$×2×2$\sqrt{3}$
=$\frac{16π}{3}$+2$\sqrt{3}$,
故答案为:$\frac{16π}{3}$+2$\sqrt{3}$.
点评 本题考查的是扇形面积的计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.


科目:初中数学 来源: 题型:填空题
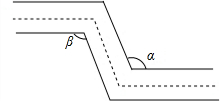 如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是内错角相等,两直线平行.
如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是内错角相等,两直线平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 3条或4条 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,AD和BC的关系为AD垂直平分BC.
如图,是一个三角形测平架,已知AB=AC,在BC的中点D挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,AD和BC的关系为AD垂直平分BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
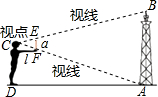 如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.
如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com