
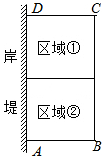
 为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米
为了节省材料,某水产养殖户利用水库的岸堤为一边,用总长为a米(a为大于21的常数)的围网在水库中围成了如图所示的①②两块矩形区域.已知岸堤的可用长度不超过21米.设AB的长为x米,矩形区域ABCD的面积为y平方米分析 (1)设AB的长为x米,则BC的长为(a-3x)米,根据矩形民机公式可得函数解析式,由0<BC≤21可得x的范围;
(2)将a=30代入解析式配方成顶点式,结合x的范围可得最值;
(3)将a=48代入解析式配方成顶点式,结合x的范围可得最值.
解答 解:(1)设AB的长为x米,则BC的长为(a-3x)米,
根据题意得:y=x(a-3x)=-3x2+ax,
由a-3x≤21可得x≥$\frac{a-21}{3}$,
由a-3x>0得x<$\frac{a}{3}$,
∴$\frac{a-21}{3}$≤x<$\frac{a}{3}$;
(2)当a=30时,y=-3x2+30x=-3(x-5)2+75,
∵3≤x<10,
∴当x=5时,y取得最大值为75;
(3)当a=48时,y=-3x2+48x=-3(x-8)2+192,
∴当x=8时,y取得最大值为192.
点评 本题主要考查二次函数的应用,根据矩形面积公式得出函数解析式,利用二次函数的顶点式,结合二次函数的性质得出其最值情况是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
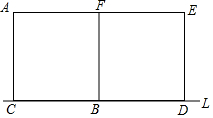 如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:
如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com