
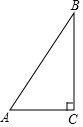
 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
科目:初中数学 来源: 题型:选择题
| A. | ${({-\sqrt{2}})^2}$=2 | B. | $\sqrt{{{({-5})}^2}}$=-5 | C. | $\sqrt{2}÷\sqrt{6}=\sqrt{3}$ | D. | $\sqrt{{a^2}b}=a\sqrt{b}({a<0})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
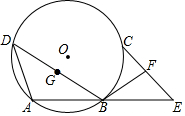 如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.
如图,点A、B、C、D在⊙O上,且$\widehat{AD}$=$\widehat{BC}$,E是AB延长线上一点,且BE=AB,F是EC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2+a3=a5 | B. | a6÷a3=a2 | C. | (2xy2)3=6x3y6 | D. | (-xy)5÷(-xy)2=-x3y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.
已知平面直角坐标系中,开口向上的抛物线与x轴交于A(2,0)、B(4,0)两点,设抛物线的顶点为M,∠AMB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com