分析:由于△P
1OA
1是等腰直角三角形,可知直线OP
1的解析式为y=x,将它与y=
联立,求出方程组的解,得到点P
1的坐标,则A
1的横坐标是P
1的横坐标的两倍,从而确定点A
1的坐标;由于△P
1OA
1,△P
2A
1A
2都是等腰直角三角形,则A
1P
2∥OP
1,直线A
1P
2可看作是直线OP
1向右平移OA
1个单位长度得到的,因而得到直线A
1P
2的解析式,同样,将它与y=
联立,求出方程组的解,得到点P
2的坐标,则P
2的横坐标是线段A
1A
2的中点,从而确定点A
2的坐标;依此类推,从而确定点A
10的坐标.
解答:
解:过P
1作P
1B
1⊥x轴于B
1,
易知B
1(2,0)是OA
1的中点,
∴A
1(4,0).
可得P
1的坐标为(2,2),
∴P
1O的解析式为:y=x,
∵P
1O∥A
1P
2,∴A
1P
2的表达式一次项系数相等,
将A
1(4,0)代入y=x+b,
∴b=4,
∴A
1P
2的表达式是y=x-4,
与y=
(x>0)联立,解得P
2(2+2
,-2+2
).
仿上,A
2(4
,0).
P
3(2
+2
,-2
+2
),A
3(4
,0).
依此类推,点A
n的坐标为(4
,0)
故点A
10的坐标是(4
,0).
故答案为:(4
,0).
点评:本题的关键是找出求P点坐标的规律,以这个规律为基础求出P10的横坐标,进而求出A10的横坐标的值,从而可得出所求的结果.


 解:过P1作P1B1⊥x轴于B1,
解:过P1作P1B1⊥x轴于B1,

 计算高手系列答案
计算高手系列答案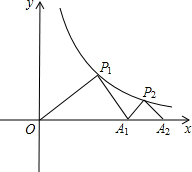 如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y=
如图,△P1OA1,△P2A1A2是等腰直角三角形,点P1,P2在函数y=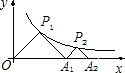 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y= 如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y=
如图,△P1OA1,△P2A1A2,△P3A2A3,…,是等腰直角三角形,点P1,P2,P3,…,在反比列函数y= 如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数y=
如图,△P1OA1、△P2A1A2、△P3A2A3、…、△P100A99A100是等腰直角三角形,点P1、P2、P3、…、P100在反比列函数y= 如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=
如图,△P1OA1、△P2A1A2是等腰直角三角形,点P1、P2在函数y=