
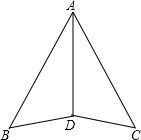
 已知:如图,AD平分∠BAC,∠B=∠C.求证:BD=CD.
已知:如图,AD平分∠BAC,∠B=∠C.求证:BD=CD.科目:初中数学 来源: 题型:
 如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,
如图在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上.若BC=8cm,AD=6cm,查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ACB中,∠C=90°,CD⊥AB,垂足为点D.
如图,在Rt△ACB中,∠C=90°,CD⊥AB,垂足为点D.查看答案和解析>>
科目:初中数学 来源: 题型:
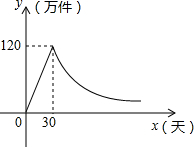 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现己知上市30天时,当日销售量为120万件.
某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现己知上市30天时,当日销售量为120万件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com